Um sistema é constituído por duas partículas de massas e , presas às extremidades de uma mola de constante elástica . O sistema está inicialmente em repouso em uma mesa horizontal sem atrito e a mola encontra-se na sua posição natural, como mostrado na figura. No instante começam a atuar duas forças constantes de mesmo módulo como indicado na figura. Utilizando os unitários relativos ao sistema de eixos indicado na figura determine:

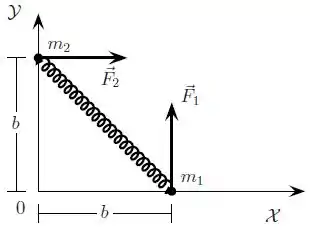
a) O vetor posição do centro de massa do sistema quando este se encontra em repouso.

b) O vetor posição do centro de massa para um instante posterior a .

Vamos calcular cada uma dessas coordenadas do centro de massa.

As coordenadas da posição de cada partícula são:

Começando em :

Já a coordenada :

Temos então que a posição do centro de massa é:

Ou então, vetorialmente usando os unitários e :

Agora que já sabemos a posição do centro de massa nesse instante inicial, podemos analisar o movimento do próprio centro de massa a partir das forças atuando no sistema.

Como assim?

Lembra da segunda lei de Newton?

Nós podemos aplicar essa lei para o centro de massa e descobrir a aceleração do centro de massa:

Sendo a massa total do sistema.

Vamos trabalhar vetorialmente, para não extender muito as contas.

Como os corpos estão num plano horizontal, as forças peso e normal se anulam.

Assim, o vetor força resultante será apenas a soma daquelas duas forças:

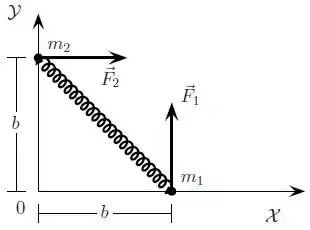
A força está na direção positiva de enquanto está na direção positiva de :

Aplicando na segunda lei de Newton, temos:

Como temos uma aceleração constante, vamos usar a equação da posição para um movimento uniformemente acelerado:

Escrevendo de forma vetorial, temos:

Já sabemos a posição inicial:

Além disso, o sistema parte do repouso:

Então, para o centro de massa temos:

Juntando as componentes e :