Um homem de sentado na popa de uma canoa de e de comprimento, conseguiu trazê-la para uma posição em que está parada, encostada perpendicularmente a um pequeno ancoradouro. Na proa da canoa encontra-se a sua namorada (). Se os dois trocarem de lugar, de que distância a canoa se afastará do ancoradouro?

Passo 1
O primeiro passo é nomear tudo para podermos diferencias as variáveis nos nossos cálculos.
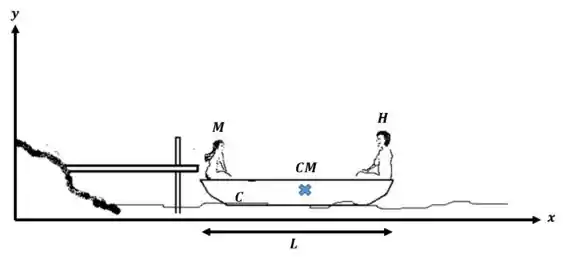
E como não há ação de forças externar sabemos que a posição do centro de massa não irá mudar, pois a velocidade do centro de massa é zero.
Passo 2
Agora vamos calcular as posições inicias e finais do centro de massa utilizando a fórmula
Como só há movimento em não precisamos representar como vetor.
Ótimo, agora a posição final do centro de massa, para isso vamos considerar que a canoa andou uma distância
Passo 3
O sistema considerado é o homem, a mulher e o barco. No momento em que o homem troca de lugar com a mulher, apenas forças internas atuam no barco, são forças do homem no barco, da mulher no barco e vice-versa. Todas forças internas.
Mas nenhuma dessas forças é externa ao sistema .
Portanto, se lembramos da regra que diz que quando o , o centro de massa permanece no mesmo lugar, nós poderemos igualar
Lembrando que corresponde à distância que o barco se afastará do ancoradouro.
Agora podemos fazer as substituições das variáveis pelos valores dados no problema.