Um arranjo experimental de interferência de fenda dupla (incluindo fonte de luz, fendas e anteparo) é observado no ar. Depois ele é todo submergido em água e novamente observado. Como o padrão de franjas se modifica?
- Nada muda, ele permanece igual.
- Todas as franjas se deslocam para um mesmo lado, assim como os raios de luz são desviados ao penetrarem numa piscina.
- As franjas se afastam umas das outras.
- As franjas de cada lado do máximo central todas se afastam juntas deste, mantendo sua distância relativa.
- As franjas se aproximam umas das outras.
Passo 1
Cara, temos aqui um problema de fenda dupla. Sabemos pela teoria que um problema de fenda dupla é mais ou menos assim, você faz passar por uma parede com dois furos uma luz proveniente de uma fonte...
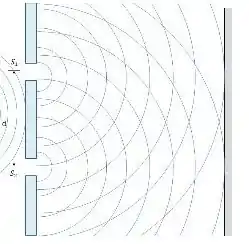
O padrão luminoso que você vai observar nesse anteparo que está a uma distância vai ser...

Ou seja, se cria faixas claras e escuras. E esse padrão acontece justamente por causa das interferências construtivas (faixas claras) e interferências destrutivas (faixas escuras). Bem Rubro Negro kkkkkk.
Mas o interessante é que a distância entre uma faixa clara e a faixa escura adjacente a ela (distância ) pode ser dado por...
Onde é a distânciazinha dos dois buracos e é a distância entre uma parede e outra. é o comprimento de onda da luz.
E o que a gente vai ver nesse problema é se a distância aumenta ou diminui. Bora?
Passo 2
Cara, o problema nos disse que a gente pegou o experimento que estava no ar...
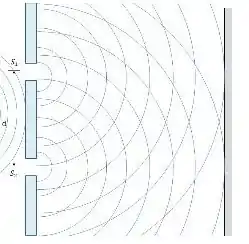
E depois fez o mesmo experimento depois, mas dentro d’água.
Ora, sabemos que pela teoria, a velocidade da luz é , e ainda sabemos que a velocidade da luz depende do meio inserido...
“Ta, mas e daí?”
Bem... E daí que na água, o índice de refração é maior que o índice de refração no ar. Ou seja, isso significa que a luz vai ter uma velocidade menor na água que no ar.
Como a frequência depende apenas da fonte, podemos dizer que se a velocidade cai por um fator de , o comprimento de onda também cai por um fator de ...
Onde ar representa o comprimento de onda no ár e água, o comprimento na água.
Passo 3
Estamos chegando no cerne da questão, porque se o comprimento de onda na água é menor que o comprimento de onda no ar, então a distância entre as franjas claras e escuras...
Também se reduz por um fator de , ou seja, as franjas se aproximam!
Resposta
Letra E.