Duas antenas estão posicionadas em um plano, com coordenadas cartesianas e . As antenas emitem ondas de radio com comprimento de onda de , em fase.
Para distâncias positivas , quanta são as direções, a partir da origem, para as quais a intensidade da radiação transmitida é máxima (interferência construtiva)?
Passo 1
Ok, temos duas antenas posicionada em e , e queremos ver a interferência dos sinais uma distância (muito maior que a distância entre as antenas).
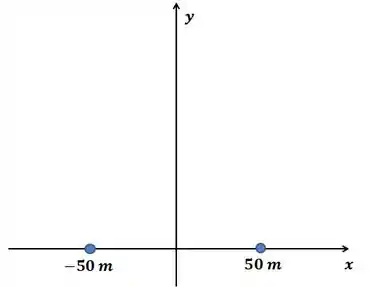
Precisamos então saber a diferença de percurso entre o sinal das duas antenas, pra podermos saber se a interferência é construtiva ou destrutiva.
Como fazemos isso? Bem, deixa eu dar uma girada na imagem pra deixar ela mais sugestiva.
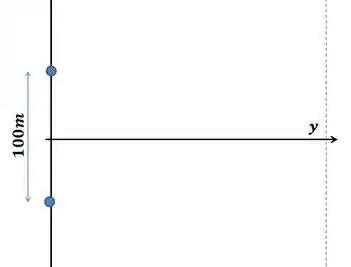
Pronto, agora olhando pra essa imagem: Que tipo de problema a gente conhece onde temos dois pontos que agem como fontes de luz e que precisamos saber qual a interferência a uma distância muito grande deles, num “anteparo”?
Bem, na verdade esse problema é bem semelhante à interferência por duas fendas pontuais!
Assim, a diferença de fase vai ter o mesmo formato, sendo o ângulo em relação ao eixo . Para interferência construtiva:
Onde é a distância entre as fontes.
Passo 2
Ok, montamos a situação do problema. Já foi meio caminho andado. Agora precisamos saber qual é o problema.
Ele pergunta “quantas são as direções onde temos máximo de interferência”. Esse problema então é de “quantas franjas aparecem no anteparo”. Para acharmos isso, fazemos o limite:
Com isso:
Logo, o último máximo que aparece corresponde a . Temos assim 7 máximos:
Nesses problemas, podemos sempre lembrar da fórmula:
Onde o corresponde às franjas laterais dos dois lados da franja central, e o contabiliza essa franja central.
Respsta é a letra .
Resposta
Letra