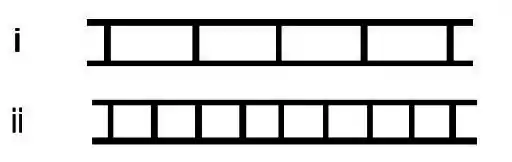
A figura (i) mostra um padrão de dupla fenda obtido usando luz monocromática. Considere as
seguintes cinco possíveis mudanças nas condições do experimento:
1. diminuir a frequência
2. aumentar a frequência
3. aumentar a largura de cada fenda
4. aumentar a separação entre as fendas
5. diminuir a separação entre as fendas
Qual(is) das opções acima pode(m) fazer a Figura (i) ficar igual a Figura (ii)?
- 3
- 5
- 1 e 3
- 1 e 5
- 2 e 4
Passo 1
Para que haja uma interferência completamente construtiva para duas fendas, temos que ter a seguinte condição:
Considerando que a largura da fenda seja muito menor que seu comprimento, podemos considerar que temos:
,
Onde é a distância entre cada fenda, é o comprimento da fenda e é o número de antinós.
Passo 2
Passo 3
A distância entre dois pontos de máximos, ou seja, distancia de dois antinós na onda é:
Usando a definição de velocidade, c e substituindo na fórmula descrita acima, conseguimos obter uma equação que descreve o espaçamento entre duas linhas sucessivas:
Assim para diminuir precisamos aumentar ou aumentar (separação entre as fendas).
Resposta
Letra E