Em um experimento de Young, a distância entre as duas fendas é e o comprimento de onda da luz incidente é. A tela de observação está a uma distância , e um detector de luz está posicionado em um ponto P a uma distância do centro da figura de interferência.
(a) Determine se a posição do ponto P está em um máximo ou em um mínimo de interferência, ou mais perto de um máximo ou mínimo.
Passo 1
Vamos entender visualmente o que o enunciado está falando
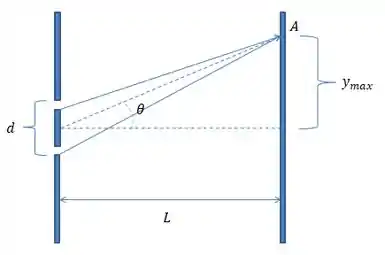
Observamos que no ponto A está ocorrendo uma interferência entre os raios, e no desenho conseguimos compreender cada um dos dados do problema. No nosso exercício onde λ está ligado ao comprimento de onda dos raios, da distância entre as fendas e L a distância até o anteparo.
Mas o que o exercício quer?
Ele quer que determinemos a distância entre as franjas, ou seja, de quantos em quantos metros vemos uma franja clara, ou seja, ele quer basicamente a distância entre dois pontos claros.
Passo 2
Sabemos que um máximo de interferência ocorre quando podemos usar a fórmula
Em que m= 0,
Mas lembra que os ângulos que usamos são pequenos?
Com isso podemos usar a relação que diz
Essa relação só vale para ângulos pequenos.
Passo 3
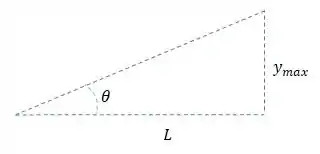
Mas pelo exemplo vemos que
E sabemos que a nossa fórmula para franjas claras é
E que para ângulos pequenos vale a relação
Substituindo teremos que
Com isso concluímos que o nosso vai ser dado pela fórmula
Sabemos pelo enunciado que
Substituindo todos esses valores na equação acharemos o valor de m. se m der um valor inteiro, significa que o nosso ponto P está próximo de uma franja clara, ou seja, um ponto de máximo. Porém se o valor der diferente de inteiro, significa que nosso ponto está próximo a uma franja escura, o que representaria um ponto de mínimo de interferência, substituindo teremos que
Isolando m teremos que
Ou seja, como dito, nosso ponto P se encontra em um ponto de mínimo de interferência.
Resposta
Temos que o ponto P está mais perto de um mínimo.