UFF, Física 3, VS 2017.2, 8
Considere a figura abaixo, que mostra a tela de visualização de um experimento de Fenda Dupla.
(i) O que acontecerá com espaçamento entre as franjas se o comprimento de onda da luz incidente for diminuído?
(ii) O que acontecerá com espaçamento entre as franjas se a distância entre as fendas e a tela for diminuída?
A) i- aumenta / ii- aumenta
B) i- aumenta / ii- diminui
C) i- diminui / ii- aumenta
D) i- diminui / ii- diminui
E) i- não se altera / ii- não se altera
Passo 1
Vamos entender visualmente o que o enunciado está falando
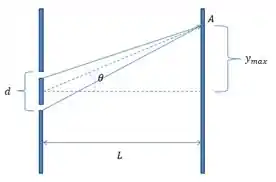
Observamos que no ponto A está ocorrendo uma interferência entre os raios, e no desenho conseguimos compreender cada um dos dados do problema. No nosso exercício onde λ está ligado ao comprimento de onda dos raios, da distancia entre as fendas e L a distancia até o anteparo.
Mas o que o exercício quer?
Ele quer que determinemos o que ocorrerá com a distância entre as franjas quando mudarmos o tamanho do comprimento de onda e a distancia até o anteparo.
Passo 2
Sabemos que um máximo de interferência ocorre quando podemos usar a fórmula
Em que m= 0,
Mas lembra que os ângulos que usamos são pequenos ?
Com isso podemos usar a relação que diz
Essa relação só vale para ângulos pequenos.
Passo 3
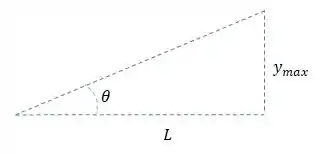Mas pelo exemplo vemos que
E sabemos que a nossa fórmula para franjas claras é
E que para ângulos pequenos vale a relação
Substituindo teremos que
Com isso concluímos que o nosso vai ser dado pela fórmula
Passo 4
Como queremos a distancia mínima entre duas franjas usaremos os valores de diferença para m=0 e m=1
Passo 5
Já com a fórmula em mãos podemos analisar cada uma das questões levantadas.
A primeira era
(i) O que acontecerá com espaçamento entre as franjas se o comprimento de onda da luz incidente for diminuído?
Como a nossa fórmula é
Vemos que se diminuirmos o comprimento de onda () o valor do nosso também irá diminuir. Então para a primeira mudança sabemos que a resposta é diminui.
Vamos para a segunda
(ii) O que acontecerá com espaçamento entre as franjas se a distância entre as fendas e a tela for diminuída?
Novamente olhando a nossa fórmula teremos que
Se diminuirmos a distância entre a tela e a fenda() vemos que também diminuiremos o valor de logo também teremos uma diminuição da distância, concluímos assim que tanto a diminuição do comprimento de onda quanto a diminuição da distância até o anteparo causara diminuição da distancia entre as franjas.
Resposta
D) i- diminui / ii- diminui