Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Interferência por Duas Fendas Pontuais

Ver Teoria
Exercício 37123456789101112131415161718192021222324252627282930313233343536383940414243

Enunciado

UFF, Física 3, P3 2017.2, 10

Duas antenas de rádio estão a 10 km de distância em um eixo norte-sul em um litoral. As antenas transmitem sinais de rádio AM idênticos, em fase, a uma freqüência de 4,70 MHz. Um navio a vapor, a 200 km de distância das antenas, viaja para o norte a uma velocidade de 15 km/h e passa a leste das antenas. Um rádio a bordo do navio é sintonizado para a frequência de transmissão. A recepção do sinal de rádio no navio é um máximo em um determinado instante. O intervalo de tempo até a próxima ocorrência de recepção máxima é aproximadamente:

A) 5,1 min

B) 3,8 min

C) 6,4 min

D) 7,7 min

E) 8,9 min

Passo 1

Nosso objetivo é calcular o tempo mínimo entre dois máximos de interferência, como já temos a velocidade do navio, Basta descobrir a distância entre esses dois máximos consecutivos e substituir os valores na fórmula de velocidade, vamos fazer isso então. Essa questão trabalha com o conceito parecido com o de fenda dupla, vamos ver uma imagem que facilite o entendimento.

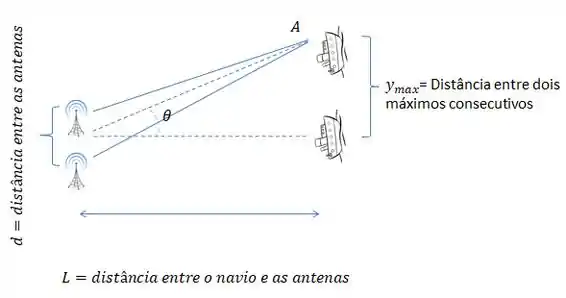
Sabemos que um máximo de interferência ocorre quando podemos usar a fórmula

d .   S e n θ = m   .   λ

Em que m= 0, ± 1 , ± 2 …

Mas lembra que os ângulos que usamos são pequenos ?

Com isso podemos usar a relação que diz

S e n   θ   ≅ T a n   θ

Essa relação só vale para ângulos pequenos.

Passo 2

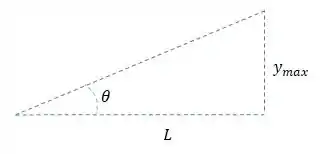Mas pelo exemplo vemos que

tan ⁡ θ = y m a x L

E sabemos que a nossa fórmula para máximos de interferência é

d .   S e n θ = m   .   λ

E que para ângulos pequenos vale a relação

S e n   θ   ≅ T a n   θ

Substituindo teremos que

d .   y m a x L = m   .   λ

Com isso concluímos que o nosso y m a x vai ser dado pela fórmula

y m a x = m   .   λ   . L d

Passo 3

Como queremos a distancia mínima entre máximos consecutivos usaremos os valores de diferença para m=0 e m=1

∆ y m a x =   λ   . L d

Sabemos que

L = 200 k m

d = 10 k m

Mas não sabemos ainda quanto vale o comprimento de onda, mas sabemos qual a fórmula que relaciona isso

Nossa amiga

v = λ . f

Sabemos que v = c = 3.10 8 m s     j á   q u e   s e   t r a t a   d e   u m a   o n d a   e l e t r o   m a g n e t i c a  

E que a frequência foi dada no enunciado, sendo ela f = 4,70 M H z = 4,70.10 6 H z

Substituindo na fórmula teremos que

3.10 8 = λ . 4,70.10 6

λ = 63,8 m = 63,8.10 - 3 k m

Passo 4

Substituindo agora na distancia entre dois máximos consecutivos teremos que

∆ y m a x =   λ   . L d

∆ y m a x =   63,8.10 - 3   . 200 10 = 1,3 k m

Agora pra calcular o tempo é simples, sabemos que o navio se move a uma velocidade de 15km/h, e que a distancia entre dois máximos principais é dada por 1,3 km, sabemos que a fórmula que relaciona eles dois é

v = ∆ s ∆ t

Substituindo os resultados teremos

15 = 1,3 ∆ t

∆ t = 0,085 h = 5,1   m i n u t o s

Resposta

a) ∆ t = 5,1   m i n u t o s

Exercícios de Livros Relacionados

No experimento de Young, com a luz incidindo perpendicularmente sobre o anteparo onde estão os dois orifícios, coloca-se uma lâmina delgada transparente de faces paralelas e índice de refração n sobre
Dois raios luminosos, inicialmente em fase e com um comprimento de onda de 500n m , percorrem diferentes trajetórias sofrendo reflexões em espelhos planos, como mostra a Fig. 35-48. (As reflexões não
Um experimento de dupla fenda produz franjas claras para a luz do sódio ( λ = 589n m ) com uma separação angular de 0,30 ° perto do centro da figura de interferência. Qual é a separação angular das fr
Um padrao de interferincia de fenda duplaeformado usando luz de laser monocromatica com comprimento de onda de 450 nm. Oque acontece com a distancia entre o primeiro maximo e o maximo central quando a
Um padrao de interferencia de fenda duplaeformado usando luz de laser monocromatica com comprimento de onda de 640 nm.No primeiro minimo do maximo central,qual ea diferenca de caminho optico entre a l