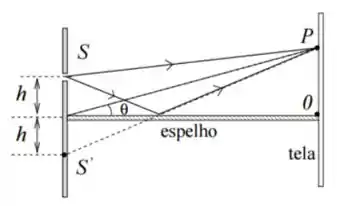
Luz monocromática de comprimento de onda incide sobre uma fenda como mostra a figura. Um espelho metálico plano está a uma distância abaixo de , muito menor que a separação entre a fenda e a tela, a qual vale . Na tela, aparecem faixas claras e escuras pela interferência entre a onda que parte de , atingindo a tela diretamente, e a onda da reflexão no espelho. Considere que, na reflexão, o feixe de luz ganha uma fase de em relação ao feixe incidente.
Em função dos dados do enunciado, calcule o que se pede. NÃO substitua os valores das constantes fundamentais na resposta final de cada item.
a) Determine o valor do ângulo na figura se a distância entre o ponto e na tela vale . Escreva sua resposta em função dos dados do problema e de , na aproximação de pequenos ângulos ().
b) Determine os valores de para os quais resultam interferência DESTRUTIVA no ponto . Escreve sua resposta em função dos dados do problema e de .
Passo 1
Fala pessoal, beleza?
Nesse problema vamos simular a situação de uma fenda e um espelho esquecendo um pouco o espelho e imaginando uma segunda fenda simétrica a primeira. Mas essa discussão vai ficar para o item (b), o item (a) é bem facinho...
Queremos relacionar o ângulo com . Para isso, consideramos o triângulo retângulo de catetos e , de modo que
Aí usamos a aproximação de pequenos ângulos:
Com isso,
Importante ressaltar que esse ângulo deve estar em radianos!
Passo 2
Já no item (b) vamos brincar com interferência. Queremos achar a defasagem entre os raios, sendo que um vai direto da fenda para a tela, enquanto o outro é refletido pelo espelho e depois chega na tela. Vamos supor que a diferença de caminho entre os dois raios é . Com isso, a defasagem entre as ondas é dada por
é a defasagem devido a diferença de caminho e é a defasagem devido à reflexão no espelho. Vale lembrar que é o número de onda, de modo que, colocando em evidência
Para que a interferência seja destrutiva, a defasagem deve ser um múltiplo ímpar de :
Assim,
Logo,
Passo 3
Mas quem é a diferença de caminho ? Podemos imaginar que o raio refletido pelo espelho tenha saído de uma fenda “imaginária” que estava abaixo do espelho, no desenho do enunciado representada por . Com isso, a diferença de caminho passa a ser
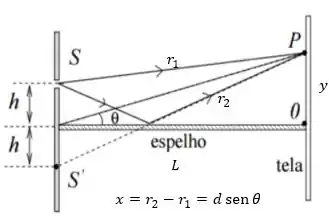
Então
Que, pela aproximação de pequenos ângulos
Assim
Observe na imagem do enunciado que é a distância entre as fendas, de modo que
Assim, substituindo na relação que achamos no passo anterior
Esses são os comprimentos de onda nos quais a interferência é destrutiva, como pediu o enunciado 😉.