Uma companhia de seguros, que trabalha no ramo de automóveis, investigou a relação entre o hábito de fumar do motorista do carro e a frequência das reclamações relativas a acidentes com danos materiais. Para isso, considerou-se as variáveis aleatórias:
número de acidentes sofridos pelo motorista (a companhia considerou de um a três acidentes) e:
Suponhamos que a companhia obteve que a distribuição conjunta de e é dada por:
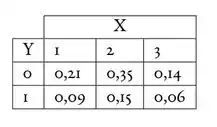
a) Determine as distribuições marginais de e
b) Podemos afirmar que o número de acidentes sofridos pelo motorista independe do fato desse ser ou não fumante?
c) Qual a probabilidade do motorista ser fumante dado que ele sofreu pelo menos dois acidentes?
Passo 1
Fala aí galera, tudo bommm?
Nessa questão temos um probleminha de distribuição conjunta de variáveis aleatórias.
Basicamente, temos todo um contextozinho sobre duas variáveis: e . A distribuição conjunta de é dada na tabela abaixo:
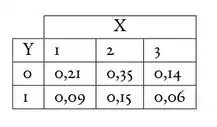
O enunciado começa nos pedindo, no item a), pra calcular as distribuições marginais de e . Vocês lembram o que é isso?

Então, a distribuição marginal de por exemplo, nada mais é do que . Ou seja, queremos montar uma tabelinha com as probabilidades para cada valor possível de .
Pra fazer isso, basta olhar a tabela da distribuição conjunta, fixar um valor de , e somar as probabilidades de quando alteramos apenas .
Conseguiu sacar a ideia?
Show! Vamo lá, mãos a obra haha.
Passo 2
Vamos começar pela distribuição marginal de .
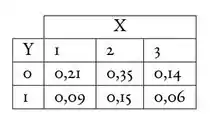
pode assumir três valores.
Se , temos:
Se , temos:
Se , temos:
Montando a tabelinha, temos:

Perfeito!
Vamos agora analisar a distribuição marginal de .
Analisando novamente a tabela de distribuição conjunta:
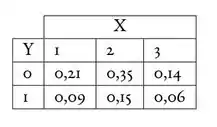
Se , temos:
Se , temos:
Show! Agora é só montar a tabelinha!
![]()
É isso aí galera! Essas são as distribuições marginais de e .
Bora pro item b).
Passo 3
No item b), o enunciado nos pergunta se podemos afirmar que o número de acidentes sofridos pelo motorista é independente do fato dele ser fumante ou não.
Eaí, o que vocês acham?

Então pessoal, bora dar uma olhada novamente na distribuição marginal de .
![]()
Quando , o motorista é fumante. Mas, olhando os resultados, vemos que a probabilidade de ocorrer um acidente é muito maior no caso dos motoristas que não fumam (probabilidade de ), do que no caso dos motoristas que fumam (probabilidade de ).
Sendo assim, chegamos a conclusão que o número de acidentes sofridos pelo motorista independe do fato dele ser fumante ou não.
Passo 4
Pra finalizar, a questão nos pede para calcular qual a probabilidade do motorista ser fumante dado que ele sofreu pelo menos dois acidentes.
Bom, vamos analisar nossa tabelinha querida haha.
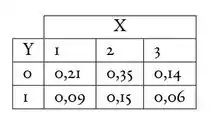
Como estamos falando de dois ou mais acidentes estamos olhando para as colunas de e .
Devemos lembrar que a questão nos pede para calcular uma probabilidade condicional. Que tem aquela formulinha:
Assim, nesse contexto é o motorista ser fumante e sofrer dois ou mais acidentes. Ou seja:
Já o conjunto se refere ao motorista, independente de ser fumante ou não, sofrer dois ou mais acidentes. Ou seja:

Perfeito! Assim, a probabilidade do motorista ser fumante dado que sofreu dois ou mais acidentes, vale:
Portanto, a probabilidade pedida vale .
Com isso encerramos mais uma pessoal, espero que vocês tenham curtido a solução.
Até a próxima 😊
Resposta
Resposta no texto.