Observe as seguintes representações de dois grafos G e H e responda.
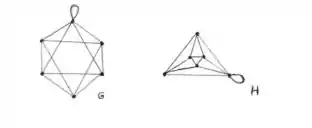
a)G é um grafo simples ou multigrafo? Justifique.
b)G e H são grafos isomorfos? Justifique.
c)Qual é a definição de grafo euleriano? Existe uma condição necessária e suficiente para sim? (Se sim descreva).
d)G é euleriano? Se sim, exiba a estrutura que satisfaz a definição, senão justifique.
e)G é bipartido? Justifique.
f)G é planar? Justifique.
g)Enuncie o Teorema de Euler que dá uma condição necessária para todo grafo planar.
h)Defina árvore
Passo 1
Eai pessoal, nessa questão o primeiro passo é enumerar os vértices do grafo G e do grafo H, fazendo a correspondência dos vértices e arestas de cada um para identificar isomorfismo.
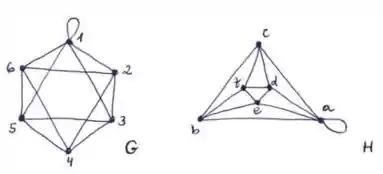
Precisamos lembrar também que grafos simples não possuem a arestas laço. Logo o grafo G não é simples, pois possui aresta laço.
Como visto na Figura podemos mostrar que:
Portanto, os grafos G e H são isomorfos já que é possível fazer correspondência entre os vértices e arestas de ambos respeitando as relações de incidência (conexões).
Passo 2
Precisamos recordar que a definição de um grafo euleriano diz que se é possível construir um ciclo que use cada aresta do grafo exatamente uma vez, então o grafo é euleriano.
Como G não tem arestas:
, sendo d(v) o grau de v.
Para descrever o ciclo de G, basta citar apenas os vértices pois não temos arestas em paralelo, começando pelo laço: equivalente à em H.
Outra condição importante é que para um grafo ser bipartido não pode possuir circuito de comprimento ímpar, logo G não é bipartido por conta do circuito 1,3,5,1 por exemplo. Além disso, G não é planar já que possui uma representação (grafo H) em que suas arestas não se cruzam.
Para enunciar o teorema de Euler que dá condição necessária vamos supor G planar. Se G é um grafo planar, então temos
é o número de faces de uma representação plana
é o número de componentes conexos de G.
Por fim, uma árvore é um grafo conexo sem circuito ou um grafo minimamente conexo. Portanto, árvore é um grafo G no qual , existe um único u-v caminho em G.
Resposta
a) G não é grafo simples, é multigrafo, pois tem aresta laço ( incidente a apenas um v )
b) Sim,é possível fazer correspondência entre os vértices e arestas de ambos respeitando as relações de incidência (conexões). Como não temos arestas em paralelo basta corresponder os vértices.
c) Um grafo é euleriano se é possível construir um ciclo que use cada aresta do grafo exatamente uma vez, então o grafo é euleriano. G não tem aresta., sendo d(v) o grau de v.
d) Sim, vamos descrever o ciclo citando apenas os vértices pois não temos arestas em paralelo, começando pelo laço: equivalente à em H.
e)Não, G não é bipartido já que possui circuito de comprimento ímpar como 1,3,5,1.
f) G não é planar já que possui uma representação (grafo H) em que suas arestas não se cruzam.
g) Se G é um grafo planar, então temos
é o número de faces de uma representação plana
é o número de componentes conexos de G.
h) Uma árvore é um grafo conexo sem circuito ou um grafo minimamente conexo. Portanto, árvore é um grafo G no qual , existe um único u-v caminho em G.