Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução à Estatística

Ver Teoria
Exercício 27123456789101112131415161718192021222324252628293031

Enunciado

UFRJ; Sem campus; probest; P1; 2022.2; Questão 4

Seja o vetor aleat ́orio bidimensional ( X ,   Y   ) , os valores possíveis tanto de X quanto de Y pertencem a { − 1 ,   0 ,   1 } . Sabe-se que a probabilidade conjunta, é tal que:

  p ( X , Y   ) ( x ,   y ) = 0.15 ;   s e ( x ,   y )   ∈   { ( − 1 ,   − 1 ) , ( − 1 ,   1 ) , ( 1 ,   − 1 ) , ( 1 ,   1 ) }

= 0.4 ;   s e ( x ,   y )   ∈   { ( 0 ,   0 ) }

= 0 ;   c . c  

Calcule:

(a) os valores esperados,   E ( X ) ,   E ( Y ) e também as variâncias, V a r ( X )   e   V a r ( Y ) ;

(b) a covariância, C o v ( X , Y ) .   X   e   Y São variáveis aleatórias independentes?

(c) a função de probabilidade condicional de X dado que Y   =   1 , ou seja p ( x | Y   =   1 ) .

Passo 1

Fala pessoal, tudo bem com vocês vamos para mais uma questão de probest.Dessa vez vamos trabalhar com as distribuições marginais de uma variável discreta. Lembram como calculamos as marginais nesse caso?

Para calcular a marginal em X nós fixamos o valor em x e somamos todos os valores variando y . Fica da seguinte forma:

  p ( X , Y   ) ( x ,   y ) = 0.15 ;   s e ( x ,   y )   ∈   { ( − 1 ,   − 1 ) , ( − 1 ,   1 ) , ( 1 ,   − 1 ) , ( 1 ,   1 ) }

= 0.4 ;   s e ( x ,   y )   ∈   { ( 0 ,   0 ) }

= 0 ;   c . c  

Então:

P X ( X = x ) = ∑ y   p ( X , Y   ) ( x ,   y )

Vamos fazer as contas aqui, para x = - 1

P X ( X = - 1 ) = ∑ y   p ( X , Y   ) ( - 1 ,   y )

p ( X , Y   ) ( - 1 ,   - 1 ) + p ( X , Y   ) ( - 1 ,   0 ) + p ( X , Y   ) ( - 1 ,   1 )

= 0.3

Vamos fazer as contas aqui, para x = 0

P X ( X = 0 ) = ∑ y   p ( X , Y   ) ( 0 ,   y )

p ( X , Y   ) ( 0 ,   - 1 ) + p ( X , Y   ) ( 0 ,   0 ) + p ( X , Y   ) ( 0 ,   1 )

= 0.4

E temos que para x = 1

P X ( X = 1 ) = ∑ y   p ( X , Y   ) ( 1 ,   y )

p ( X , Y   ) ( 1 ,   - 1 ) + p ( X , Y   ) ( 1 ,   0 ) + p ( X , Y   ) ( 1 ,   1 )

= 0.3

De forma análoga, podemos calcular

P Y ( Y = y )

Passo 2

Agora que temos a nossa distribuição marginal em X e sabemos calcular a distribuição marginal em Y podemos montar uma tabelinha contendo essas informações

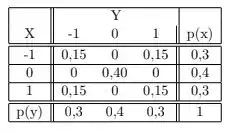
Onde a parte do meio é a probabilidade conjunta de X ,   e   Y e as colunas externas as marginais. Note que calcular as marginais pela tabela é mais simples. Para a marginal de X somamos as linhas, e para a de Y as colunas

Bem, agora que temos as marginais. Vamos começar a questão. A letra a pede os valores esperados,   E ( X ) ,   E ( Y ) e também as variâncias, V a r ( X )   e   V a r ( Y ) ;

Bem, por definição

  E ( X ) = ∑ x x p ( x )

= - 1 * 0.3 + 0 * 0.4 + 1 * 0.3

= 0

  E ( Y ) = ∑ y y p ( y )

= - 1 * 0.3 + 0 * 0.4 + 1 * 0.3

= 0

E suas variâncias são

V a r ( X ) = E [ X 2 ] - E [ X ] 2

= E [ X 2 ]

Usando o estatístico preguiçoso

= ∑ x x 2 p ( x )

= 0.3 + 0 + 0.3

= 0.6

V a r ( Y ) = E [ Y 2 ] - E [ Y ] 2

= E [ Y 2 ]

Usando o estatístico preguiçoso

= ∑ y y 2 p ( y )

= 0.3 + 0 + 0.3

= 0.6

Passo 3

Vamos para a letra b ) precisamos da covariância, C o v ( X , Y ) .   X   e   Y São variáveis aleatórias independentes?

Bem, por definição.

C o v ( X , Y ) = E [ X Y ] - E [ X ] E [ Y ]

Mas como já calculamos a esperança de E [ X ] temos que

C o v ( X , Y ) = E [ X Y ]

Usando estatístico preguiçoso, temos que

E [ X Y ] = ∑ x , y x y p ( X , Y   ) ( x ,   y )

Mas pela n ossa tabela de probabilidade

∑ x , y x y p ( X , Y   ) ( x ,   y ) = ( - 1 ) * ( - 1 ) 0.15 + ( 1 ) * ( 1 ) * 0.15 + ( 1 ) * ( - 1 ) 0.15 + ( - 1 ) * ( 1 ) 0.15

= 0

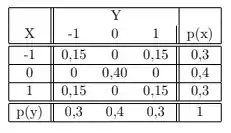
Ou seja, C o v ( X , Y ) = 0

Mas essas variáveis são independentes? Para temos independência a definição diz que a distribuição conjunta das variáveis é o produto de suas marginais, contudo

p ( X , Y   ) ( − 1 ,   − 1 )   =   0 ,   15 ≠   p X ( − 1 )   ×   p Y   ( − 1 )   =   0.3   ×   0.3   =   0.09 .

Logo as variáveis não são independentes.

Passo 4

Para finalizar, a letra c ) . Queremos a função de probabilidade condicional de X dado que Y   =   1 , ou seja p ( x | Y   =   1 ) . Ora, mas por definição

p ( x | Y   =   1 ) = P X , Y ( x , y = 1 ) / P Y ( y = 1 )

usando a nossa tabelinha,

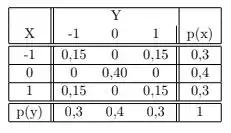
Temos que

p ( x = - 1 | Y   =   1 ) = P X , Y ( x = - 1 , y = 1 ) / P Y ( y = 1 )

= 0.15 / 0.3

= 0.5

p ( x = 0 | Y   =   1 ) = P X , Y ( x = 0 , y = 1 ) / P Y ( y = 1 )

= 0

p ( x = 1 | Y   =   1 ) = P X , Y ( x = 1 , y = 1 ) / P Y ( y = 1 )

= 0.15 / 0.3

= 0.5

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Desenvolvimento Acima

Exercícios de Livros Relacionados

Faça um experimento de simulação usando um pacote estatístico ou outro software para estudar a distribuição de X - quando a distribuição da população é lognormal com E l n X = 3 e V l n X = 1 . Consid
Faça um experimento de simulação usando um pacote estatístico ou outro software para estudar a distribuição de X - quando a distribuição da população é Weibull com α = 2 e β = 5 , como no Exemplo 5.19
Tabela de números aleatóriosUse a décima linha da Tabela B.1 para gerar 10 números aleatórios entre 1 e 920.
Vinte e uma pacientes de uma clínica médica tiveram o seu nível de potássio no plasma medido. Os resultados foram os seguintes:Construa o histograma.Determine os 1°, 2° e 3° quartis.Qual a porcentagem
O conjunto de dados representa o número de filmes assistidos em um ano por uma amostra de 24 pessoas.121 148 94 142 170 88 221 106 186 85 18 106 67 149 28 60 101 134 139 168 92 154 53 66(d) Descreva a