Suponha que um dado honesto seja rolado duas vezes. Quais são os possíveis valores que as seguintes variáveis aleatórias podem assumir e qual a distribuição de probabilidade associada à cada uma delas?
a) O máximo valor que aparece nas duas vezes em que o dado é jogado.
b) O valor da primeira jogada subtraído do valor da segunda jogada.
Passo 1
Oii gente, tudo bomm?
O enunciado é bem direto com a gente. Um dado é lançado duas vezes e seus valores são anotados.
A partir disso, vamos definir duas variáveis aleatórias:
a) máximo valor entre os dois lançamentos.
b) Valor da primeira jogada subtraído do valor da segunda jogada.
Sobre e queremos saber quais os valores que eles podem assumir, e também qual a distribuição de probabilidade que relaciona cada uma dessas variáveis!
Então, vamos primeiro interpretar os possíveis valores que podem ser assumidos. A partir disso, pra cada valor possível, calculamos a probabilidade associada e usamos aquela tabelinha pra expressar a distribuição associada a cada variável aleatória. Beleza?

Passo 2
Bom, vamos começar analisando nossa variável aleatória :
máximo valor entre os dois lançamentos
Então pessoal, se lançamos um dado ele pode nos dar:
Lançando o dado duas vezes, não muda o fato que esses são os possíveis valores.
A variável pede o maior valor entre os dois lançamentos. Como o valor do lançamento com certeza está de a , o máximo valor também estará.
Portanto, os possíveis valores para são:
Perfeito!
E, quanto à distribuição de probabilidade, o dado é honesto, então cada um desses valores é equiprovável.
Mesmo que a gente esteja considerando esses valores em dois lançamentos, os resultados continuam sendo equiprováveis pelo fato do dado ser honesto.
(Tá vendo galera? Não é só sobre matemática, é lição de vida mesmo! haha)
Portanto, cada uma desses valores possui a probabilidade:
Montando a tabelinha de distribuição de probabilidade, temos:

Prontinho! Quanto a já terminamos nosso trabalho 😊
Passo 3
Agora vamos para !
Valor da primeira jogada subtraído do valor da segunda jogada
Aqui temos um pouquinho mais de trabalho. Para determinar os possíveis valores de precisamos analisar essas subtrações. A dica é procurar as subtrações com os menores e maiores valores possíveis.
Vamos buscar o menor valor possível.
Para isso, podemos dizer que o primeiro dado assumiu o seu menor valor, ou seja, . E, o segundo dado, assumiu o seu maior valor, ou seja, . Logo:
Massa! Para encontrar o maior valor basta invertermos as posições, o primeiro dado vale e o segundo vale . Logo:
Assim, os possíveis valores vão de a .
Excelente!
Passo 4
Agora vamos buscar a distribuição de probabilidade associada.
Para fazer esse cálculo, vamos montar uma tabela que nos dê todas as possíveis subtrações:
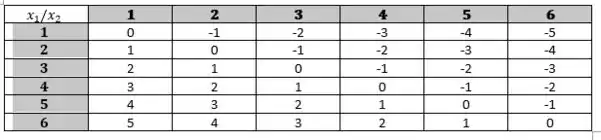
onde a coluna representa os valores do lançamento do dado, e a linha os valores do lançamento do dado. E, o resultado da subtração está expresso no cruzamento das informações.
Perfeito! Agora que fizemos isso podemos usar a definição de probabilidade pra realizar os cálculos.
Analisando a tabela, temos subtrações possíveis. Então:
O número de casos favoráveis depende de qual valor de estamos considerando. Se analisarmos , por exemplo, pela tabela vemos que se repete vezes. Ou seja:
Entendeu a ideia?
Fazendo isso podemos montar maaais uma tabelinha haha:

Prontinho! Matamos mais uma questão!
Curtiu a solução? Responde Aí!
Resposta
Resposta no texto.