Dadas as seguintes informações;
Um por cento das mulheres tem câncer de mama.
Noventa por cento das mulheres que têm câncer de mama testam positivo em mamografias.
Oito por cento das mulheres terão falsos positivos.
a) Qual a probabilidade de uma mulher obter o resultado positivo para câncer de mama?
b) Qual é a probabilidade de uma mulher ter câncer se ela tiver um resultado positivo na mamografia?
Passo 1
Fala aí gente, tudo bem?
Essa questão traz algumas afirmações acerca do câncer de mama em mulheres. Essas afirmações estão relacionadas a probabilidades da mulher ter, ou não, câncer de mama. E devemos usá-las para determinar:
No item a), a probabilidade de uma mulher obter um resultado positivo. (perceba que ela não necessariamente tem câncer, um falso positivo ainda é um resultado positivo).
No item b), a probabilidade condicional da mulher ter câncer se ela tiver um resultado positivo.

É galera, sei que fica um pouco confuso com tantas informações e pedidos.
O ideal é a gente ir analisando cada uma das afirmações do enunciado com calma, e tentar montar uma árvore de probabilidades para a partir daí responder as perguntas.
Então, vamo lá!
Passo 2
Pra começar é falado que das mulheres têm câncer de mama. Assim, podemos separar o universo das mulheres em dois ramos:
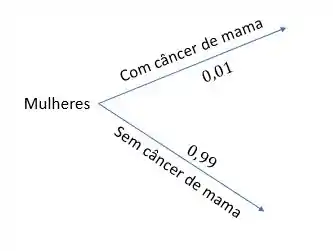
Beleza, a próxima afirmação diz que das mulheres que possuem câncer de mama, testam positivo. Assim, separamos o universo das mulheres que possuem câncer de mama em dois novos ramos:
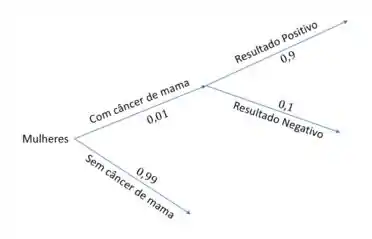
Por fim, a última afirmação fala que dentre as mulheres sem câncer de mama, apresentam falso positivo. Ou seja, o grupo de mulheres sem câncer de mama será dividido novamente entre aquelas que são falso positivo no exame, e as que não são:
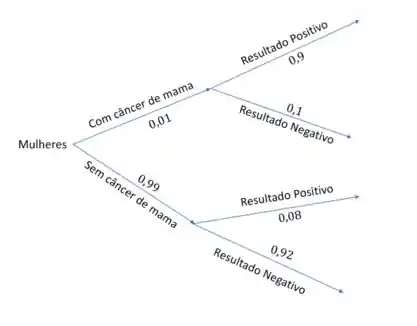
Olha que legal! Com isso finalizamos nossa árvore de probabilidades.
Vamos então para as perguntas!
Passo 3
No item a) devemos verificar a probabilidade de uma mulher testar positivo para o câncer de mama.
Analisando a nossa árvore, vemos que há dois ramos, ou seja, dois grupos de mulheres que testam positivo:
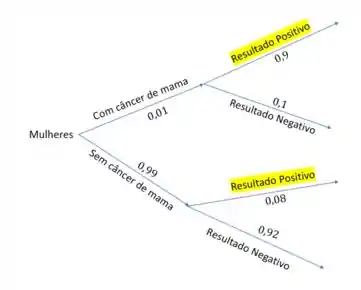
Para calcularmos as probabilidades relativas a esses ramos, basta fazermos o produto das probabilidades no seu caminho.
Dentre as mulheres que possuem câncer de mama e testam positivo, por exemplo, temos uma probabilidade de:
Já dentre as mulheres que são falso positivo, temos:
Logo, a probabilidade total vale:
Excelente!
Passo 4
Aqui no item b) precisamos determinar a probabilidade da mulher ter câncer, dado que ela testou positivo no exame.
É bem a ideia de probabilidade condicional gente, é só lembrar da formulinha que:
Como vimos no passo anterior, dentre os 16,92% das mulheres que testam positivo no exame, apenas realmente possuem câncer. O restante é falso positivo.
Assim, é o grupo que testa positivo e realmente tem câncer. Ou seja:
Já o conjunto é o grupo que apresenta resultado positivo. Então:
Portanto:
Prontinhooo! Conseguimos.
Entenderam tudo direitinho? Obrigado pela atenção!
Resposta
a) ou
b) ou