O escore final num exame de proficiência na língua inglesa varia de pontos, pulando de dez em , com mais pontos indicando um melhor desempenho. Informações coletadas durante várias aplicações deste exame ao longo de anos permitem estabelecer o seguinte modelo para o desempenho no teste:
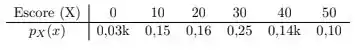
(a) Qual o valor de para que seja de fato uma função de probabilidade?
(b) Algumas universidades americanas exigem um escore mínimo de pontos para aceitar candidatos de países de língua não inglesa. Numa amostra aleatória de estudantes dentro de um grupo grande de alunos, calcule a probabilidade de pelo menos consigam satisfazer o requisito.
(c) Dentre os candidatos que realizam o teste, em geral pretendem usar o resultado em apenas uma universidade. Usando o modelo Poisson de forma aproximada, calcule a probabilidade de que numa amostra de candidatos, sorteado de forma aleat ́oria, no mínimo usarão o resultado do teste em apenas uma universidade.
Passo 1
Fala pessoal, tudo bem com vocês vamos para mais uma questão de probest. Bem, temos uma função que diz a probabilidade de alunos obterem uma certa nota em um exame.
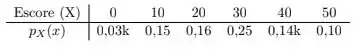
A letra pergunta qual deve ser o valor de para essa função ser uma função de probabilidade. E aí? como fazemos isso?

Ora, se esses são os valores de uma função de probabilidade, então eles tem que somar . Logo temos que
Logo
Passo 2
Vamos para a letra . Algumas universidades americanas exigem um escore mínimo de pontos para aceitar candidatos de países de língua não inglesa. Numa amostra aleatória de estudantes dentro de um grupo grande de alunos, calcule a probabilidade de pelo menos consigam satisfazer o requisito.
Ou seja, queremos a probabilidade de pelo três pessoas passarem em um grupo de . Mas a probabilidade de pessoas em 10 passarem é uma binomial, onde a probabilidade de sucesso é a probabilidade do aluno tirar mais que .

Vamos começar calculando a probabilidade de uma pessoa ser aprovada. Essa é a probabilidade do aluno tirar mais que . Que é
Olhando a nossa tabela,
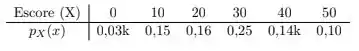
E lembrando que temos que
Logo, como queremos a probabilidade de PELO MENOS três alunos passarem, elá será dada por
Passo 3
Para finalizar, a letra . Dentre os candidatos que realizam o teste, em geral pretendem usar o resultado em apenas uma universidade. Usando o modelo Poisson de forma aproximada, calcule a probabilidade de que numa amostra de candidatos, sorteado de forma aleatória, no mínimo usarão o resultado do teste em apenas uma universidade.
Então vamos lá, precisamos fazer uma aproximação usando a poisson. Lembram como é essa distribuição?
onde é a média da distribuição.
No nosso caso, o enunciado diz que dos alunos pretendem usar o resultado em uma única universidade. Logo, em média, * alunos usarão esse resultado em uma única universidade. E essa média é a que vamos utilizar como o na nossa distribuição poisson
Dessa forma, a probabilidade de no MÍNIMO alunos usarem o resultado em uma única probabilidade é:

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento Acima