Estações de monitoramento mediram a concentração partículas inaláveis de
e a temperatura média mensal (em graus C) para cada mês de um dado ano em uma cidade. Os dados medidos seguem abaixo:

Use que
- Construa o boxplot da concentração de PM10 e interprete-o quanto a simetria e valores discrepantes.
- Usando uma medida de variabilidade adequada, compare os níveis de PM10 e a temperatura média.
(c) Obtenha a reta de regressão e interprete as estimativas dos coeficientes.
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de probest. Vamos começar pela letra
Queremos construir o boxplot da concentração de PM10 e interprete-o quanto a simetria e valores discrepantes.
Bem, como construímos um boxplot mesmo? Para isso precisamos ordenar os valores das concentrações de PM10, calcular seus quartis, e calcular os limites superiores e inferiores. Que são dados por:

Bem vamos começar a ordenar nossos dados.

Os níveis de são:
Logo seu primeiro quartil ( dos dados) é
Logo seu segundo quartil ( dos dados) é
E seu terceiro quartil ( dos dados) é
Passo 2
Agora que temos os quartis
, podemos calcular
Logo nosso boxplot será dado por:
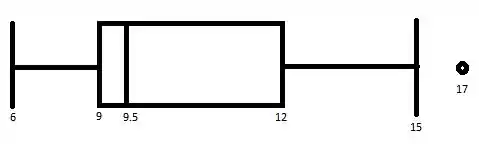
O boxplot revela uma assimetria à direita e um valor discrepante, no caso o valor .
Passo 3
Letra
Usando uma medida de variabilidade adequada, compare os níveis de PM10 e a temperatura média.
Bem, como as variáveis têm valores muito distantes entre si, por conta da própria natureza dos dados. A medida mais adequada para comparar as duas seria o coeficiente de variação. Que é dado por
Como
Temos que
Logo, com base no podemos dizer que a variável “níveis de PM10”possui maior variabilidade que a temperatura média.
Passo 4
Para finalizar, vamos para a letra Obtenha a reta de regressão e interprete as estimativas dos coeficientes.
Sabendo que
Temos que o coeficiente linear da reta de regressão é:
Substituindo os valores
O intercepto da regressão Linear é dado por
Logo, podemos observar uma relação decrescente entre os níveis de PM10 e a temperatura.

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento Acima