João, professor de probabilidade, está realizando uma pesquisa e gostaria de calcular o número de amostras possíveis que se pode obter a partir de uma população de 20 elementos se quisermos montar uma amostra aleatória com elementos sem reposição.
Passo 1
Vamos lááá!!!
O enunciado nos diz que temos uma população de 20 elementos e a partir dela queremos calcular o número de amostras que podemos ter se quisermos montar uma amostra aleatória com 15 elementos sem reposição! Repito: SEM REPOSIÇÃO! haha
Para calcular isso utilizaremos a fórmula de combinação:
Onde

Beleza... No caso aqui queremos calcular 15 elementos para montar uma amostra aleatória de um total de 20 elementos. Ou seja, combinação de 15 elementos de 20!!
Passo 2
Substituindo os valores, temos
Abrindo os fatoriais do numerador e denominador, ficamos com
Opa!! Podemos cortar o do numerador com o do denominador:
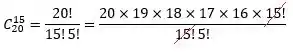
Portanto, fazendo as continhas com o que sobrou, temos
Ou seja, conseguimos obter amostras com 15 elementos sem reposição! Beleza?!