Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Operações com Conjuntos

Ver Teoria
Exercício 612345789101112131415161718192021222324252627282930313233

Enunciado

UFSC, Pré-cálculo – Lista 1 – Questão 25

Considere A = { 0,1 , 4,6 , 7,8 , 9 } , B = { 0,1 , 2,3 , 6 } e o conjunto universo U = x ∈ N         x ≤ 10   } . Faça um diagrama e, em seguida, determine:

  1. n A ∩ B
  2. n ( A ∪ B
  3. n A -
  4. n B -
  5. n A ∩ B -
  6. n ( A ∪ B ) -  

Passo 1

Faaala, galeeera! Tudo tranquilo por aí?

Primeiro vamos entender o que é diagrama de Veen-Euler. Esse diagrama basicamente é um desenho com círculos que fazemos pra representar os conjuntos. Não é nada difícil e eu vou mostrar isso pra vocês!!!

Conseguiu então captar qual é a ideia desse exercício? Ele disse pra gente que o universo é composto de todos os números naturais que vão de 0 até 10. Mas perceba que alguns números não estão dentro de A ou B, então a gente vai ter que desenhar isso no diagrama de Venn – Euler.

Passo 2

Vamos então desenhar nosso conjunto A e B e o Universo.

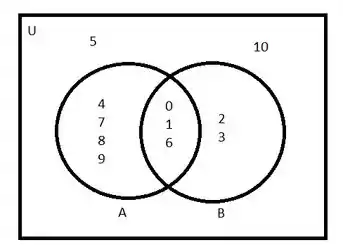
Perceba que como 5 e 10 não apareceu no conjunto A e B, ele só pode está do lado de fora das bolinhas, mas contido ainda dentro do universo U.

Passo 3

  1. Com o diagrama montado fica mais fácil de analisar quem são os elementos da intersecção né?

    2. A ∩ B = { 0,1 , 6 }

    Mas o exercício pede n ( A ∩ B ) , ou seja, a quantidade de elementos que contem esse conjunto aí. No caso, temos n A ∩ B = 3 .

    Passo 4

  2. Analogamente podemos calcular o número de elementos da união dos conjuntos

A ∪ B = { 0,1 , 2,3 , 4,6 , 7,8 , 9 }

Mas o exercício pede n ( A ∪ B ) , ou seja, a quantidade de elementos que contem esse conjunto aí. No caso, temos n A ∪ B = 9 .

Passo 4

Na letra (c) queremos o número de elementos do complementar de A, ou seja, o número de elementos total menos o número de elementos que temos somente no conjunto A. Podemos escrever da seguinte maneira:

A - B = e l e m e n t o s   e x c l u s i v o s   d e   A = 4,7 , 8,9

n U = 9   e l e m e n t o s

Logo,

n A - = n U - n A - B

n A - = 9 - 4 = 5

Passo 5

Na letra (d) queremos o número de elementos do complementar de B, ou seja, o número de elementos total menos o número de elementos que temos somente no conjunto B. Podemos escrever da seguinte maneira:

B - A = e l e m e n t o s   e x c l u s i v o s   d e   A = 2,3

n U = 9   e l e m e n t o s

Logo,

n A - = n U - n B - A

n A - = 9 - 2 = 7

Passo 6

Na letra (e) queremos o número de elementos do complementar da intersecção de A com B, ou seja, o número de elementos total menos o número de elementos que temos na intersecção. Podemos escrever da seguinte maneira:

n A ∩ B = 3

Logo,

n ( A ∩ B ) - = n U - n A ∩ B

n ( A ∩ B ) - = 9 - 3 = 6

Passo 7

Analogamente a letra (e), porém agora olhando para união, temos:

n ( A ∪ B ) - = n U - n A ∪ B

n ( A ∪ B ) - = 9 - 9 = 0

Até a próxima!

Resposta

  1. 3
  2. 9
  3. 5
  4. 7
  5. 6
  6. 0

Exercícios de Livros Relacionados

Prove que todo subconjunto do R 2 com um número finito de pontos tem conteúdo nulo.
Prove que o conjunto vazio tem conteúdo nulo.
Sejam AeB subconjuntos do R 2 com A ⊂ B . Prove que se B tiver conteúdo nulo, então A também terá.