UFSC – Pré Cálculo – Lista 2 – Questão 7d
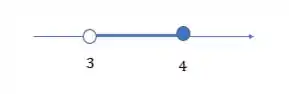
Dados os conjuntos e , efetuar as operações pedidas, dar as respostas na notação de intervalo e representar graficamente
Passo 1
E aí pessoal, tudo bem? O problema nos deu esses dois conjuntos aqui
e
E pediu para efetuar essa operação aqui apresentar a resposta em formato de intervalo e também graficamente
Mas você lembra como fazer isso?
Quando temos de dois conjuntos estamos falando da operação de diferença, isto é, queremos todos os elementos do conjunto A, menos os que são comuns ao conjunto B!
Então se temos um conjunto e outro , a diferença deles é . A ordem aqui importa viu! Se fizermos teremos , pois tiramos do todos os elementos que são comuns ao . Ok?
E se falarmos em intervalor contínuos? Muda alguma coisa! Muda sim: precisamos lembrar que bolinha vazia o elemento não está no conjunto e bolinha cheia, está. Belezinha?
A ideia para resolver essa questão é fazer um esquema dos conjuntos, verificar quais são comuns e retirar!
Show?
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Nossos conjuntos são
e
Graficamente temos:
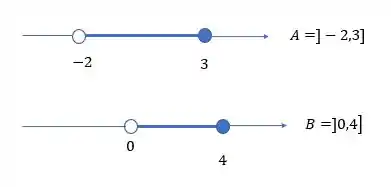
O conjunto diferença serão todos os elementos de , menos os elementos de que são comuns ao .
Tranquilo até aqui?
Vamos ver como que fica de forma gráfica essa diferença:
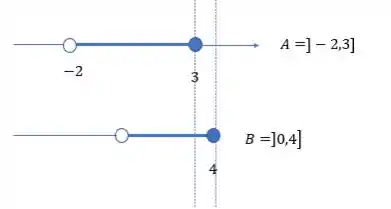
Como o está no conjunto , ele vai ser eliminado do nosso conjunto diferença! Lembra que queremos todos elementos de , mas que não estejam no . Antes do os conjuntos têm elementos comuns até o (extremo de B), então ali todos são eliminados. Ficamos com esse intervalo aqui
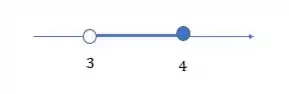
E é isso!
Espero ter ajudado! Vamos para a próxima?
Resposta
