No diagrama de Venn-Euler abaixo, cada região foi denominada com um número entre parênteses indicar as regiões que determinam:
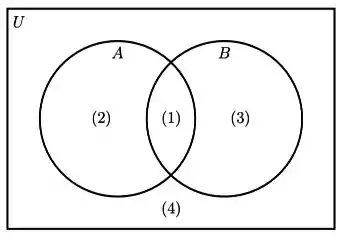
Passo 1
Amigx, se prepara porque você vai ver muito essa figura aqui no exercício hahaha BORA LÁ!
Vamos dar uma olhada no que ele pede:
Ou seja, a área comum do diagrama entre e , look at this:
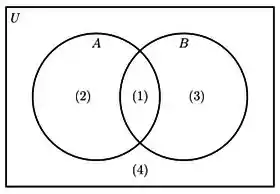
Concorda comigo que é área de número ? É a parte que pertence tanto ao conjunto quanto ao , AO MESMO TEMPO.
Passo 2
Vamos dar uma olhada no que ele pede:
Ou seja, a área toda do diagrama que representa o conjunto e o unidos, take a look:
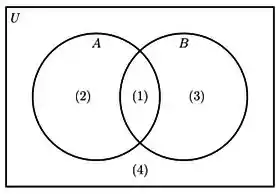
Concorda comigo que são as áreas de números ? São as partes que pertencem ao conjunto , ou ao ou aos dois.
Passo 3
Vamos dar uma olhada no que ele pede:
Ou seja, a área toda do diagrama que representa o conjunto e aí a gente tira tudo que é do conjunto também, take a look:
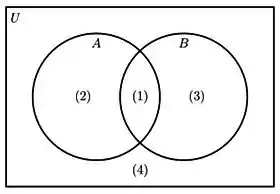
Concorda comigo que é a área de número ? É parte que pertence somente ao conjunto , sem nada do que tinha em comum com . Basicamente, é você tirar a interseção dos dois, que na figura era o número .
Passo 4
Vamos dar uma olhada no que ele pede:
Já que estamos tratando de complementar, vale dizer que o complementar de um conjunto é tudo aquilo que NÃO é o próprio conjunto. Na imagem, tenta ver quem seria o complementar de .
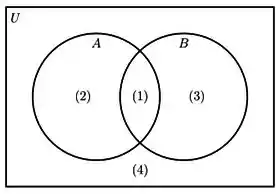
O que temos que pegar aqui são todas as áreas que NÃO são do conjunto , que no caso são as áreas de números e .
Passo 5
Vamos dar uma olhada no que ele pede:
Já que estamos tratando de complementar, vale dizer que o complementar de um conjunto é tudo aquilo que NÃO é o próprio conjunto. Na imagem, tenta ver quem seria o complementar de .
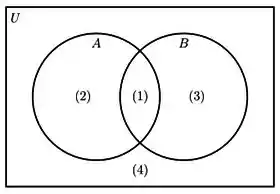
O que temos que pegar aqui são todas as áreas que NÃO são do conjunto , que no caso são as áreas de números e
Passo 6
Vamos dar uma olhada no que ele pede:
Agora que você já está cansado de ver o complementar, decidi dar uma esquentadinha. Bora tentar fazer esse? Faremos de duas formas. Primeiro, vamos resolver de dentro para fora, vamos ver quais são as áreas da união desses conjuntos:
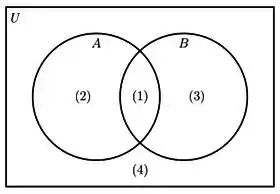
São as áreas . Agora vamos tomar o complementar delas, ou seja, vamos pegar a área que NÃO seja ela, ok? Nesse caso é a área .
Agora faremos de outra forma, usando a propriedade do complementar:
Bom, já vimos que os números que representam o complementar de são e os números que representam o complementar de são .
O número que aparece nos dois é aquele que representa a área de interseção dos complementares. No caso, o número .
Passo 7
Vamos dar uma olhada no que ele pede:
Agora que você já está cansado de ver o complementar, decidi dar uma esquentadinha. Bora tentar fazer esse? Faremos de duas formas. Primeiro, vamos resolver de dentro para fora, vamos ver quais são as áreas da interseção desses conjuntos:
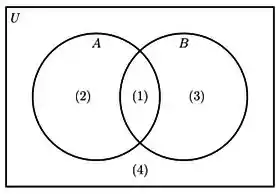
É a área . Agora vamos tomar o complementar dela, ou seja, vamos pegar a área que NÃO seja ela, ok? Nesse caso é a área representada pelos números .
Agora faremos de outra forma, usando a propriedade do complementar:
Bom, já vimos que os números que representam o complementar de são e os números que representam o complementar de são .
Se unirmos todos esses caras ficamos com .
Resposta
Ei, a resposta está no passo a passo :)