UFSC – Pré Cálculo – Lista 2 – Questão 14a
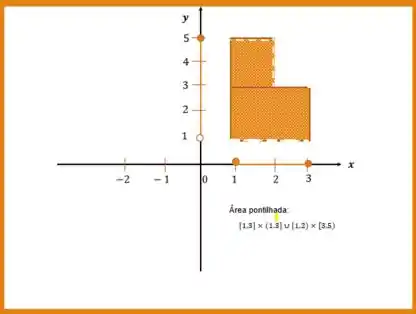
Dados os conjuntos , representa graficamente, no plano cartesiano
Passo 1
E aí pessoal, tudo bem? O problema nos esses quatro conjuntos
e pediu para representarmos graficamente o produto cartesiano no plano cartesiano . Mas, como fazer isso?
O produto cartesiano é um conjunto formado pelos pares ordenados envolvendo os elementos dos dois conjuntos dados
Ué, como assim?
Se tivermos dois conjuntos com elementos, vamos resgatar do primeiro elemento a abscissa e do segundo conjunto a ordenada do ponto
Fazendo o produto cartesiano temos que as abscissas dos pontos vêm de e a ordenada de
Então vamos ter quatro pontos! Se a ordem for trocada, vamos ter outros pontos, aqui precisamos ter atenção!
Beleza?
E se algum desses conjuntos for um intervalo? Então não vamos ter pontos e sim segmentos de retas! Isso mesmo! Aqui você precisa ter atenção se o intervalo é aberto ou fechado, isso vai ser importante no início e no fim do seu segmento (bolinha aberta ou fechada). E no caso de os dois conjuntos serem intervalos? Então teremos uma região!
Então a ideia é achar as duas regiões e, e fazer a operação
Isto é, queremos toda região que não é comum a região,
Mas relaxa, vou fazer passo a passo com você!
Passo 2
A primeira região é com os conjuntos
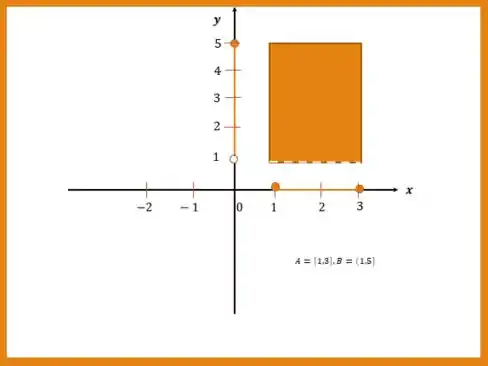
Tranquilo até aqui?
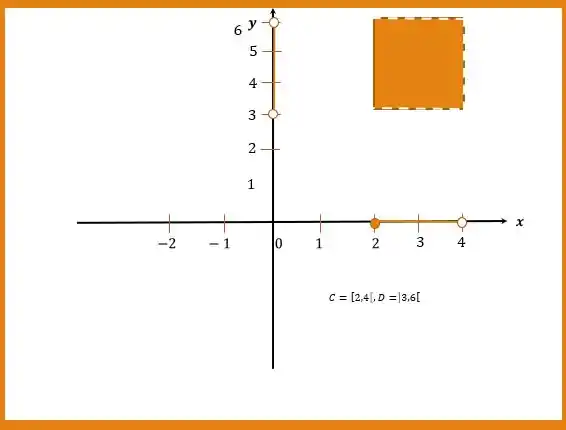
Tudo bem até aqui?
Passo 3
Nosso passo final será retirar todos os elementos da primeira região que sejam em comuns com a segunda região! Fazendo a subtração de abscissa com abscissa, e ordenada com ordenada temos
E
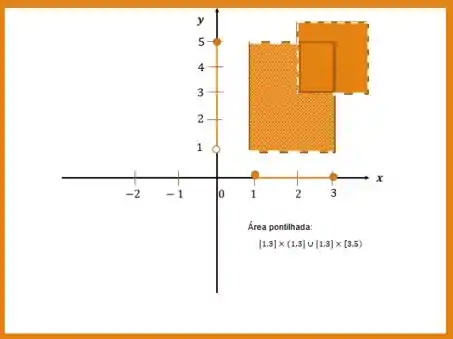
Então para descrever precisamos separar em dois produtos cartesianos:
A parte de baixo do :
E a coluna para cima:
Assim nossa região hachurada fica a união das duas:
E a representação gráfica fica assim:
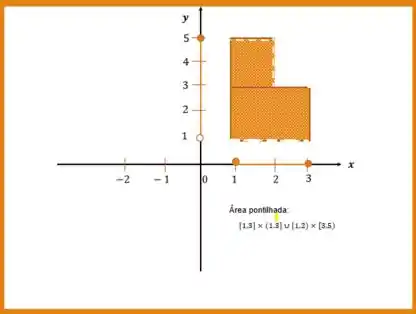
E é isso!
Espero ter ajudado! Vamos para a próxima?
Resposta
