UFSC – Pré Cálculo – Lista 1 – Questão 4
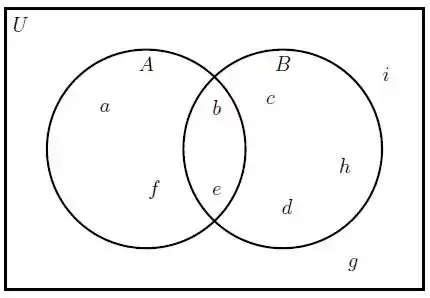
Observando o diagrama de Venn-Euler ao lado, escrever por enumeração os conjuntos:
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui!
O problema deu esse diagramam de Venn aqui embaixo
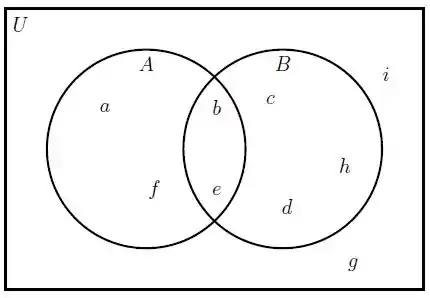
E pediu para escrevermos por enumeração (ou seja, escrever cada elemento mesmo) uma série de conjuntos
Mas o que chama atenção são duas palavrinhas que sempre aparecem: ‘ou’ e ‘e’. você lembra o que elas significam? Vou te ajudar então!
Quando temos ‘e’: significa que vamos unir os as duas condições! O elemento que estiver dentro das duas condições, então será nosso elemento! Beleza?
E quando temos ‘ou’?
Quando temos ‘ou’ significa dizer que o elemento precisa satisfazer ou a segunda! É o nosso “união”
E é isso! Com essas definições vamos encontrar os conjuntos que o problema pede!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Vamos pegar os três primeiros conjuntos:
E analisar novamente o diagrama:
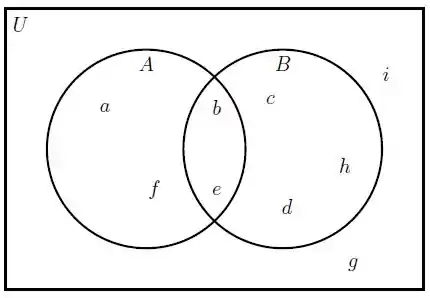
Para o conjunto C precisamos que os elementos pertençam ao A e ao B ao mesmo tempo:
Já o conjunto D é composto dos elementos que pertencem ao A ou ao B, então na prática é a união desses conjuntos:
E o conjunto E pede os elementos que pertencem ao A e que não pertencem ao B, e essas duas coisas precisam acontecer ao mesmo tempo:
Beleza?
Passo 3
Agora vamos aos próximos dois conjuntos:
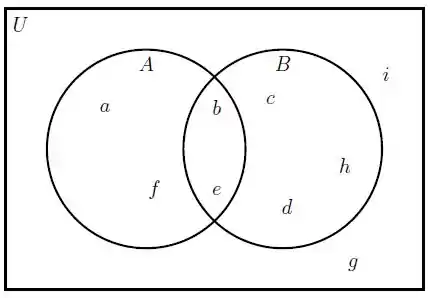
E o conjunto G? ele segue a mesma lógica, mas agora os elementos precisam pertencer ao U e não pertencer ao B, ao mesmo tempo:
Tranquilo até aqui? Vamos para os próximos?
Passo 4
Os três últimos conjuntos são:
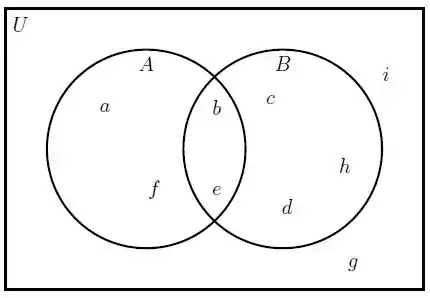Relembrando novamente do diagrama:
Agora no conjunto H ele pede todos os elementos que pertençam ao conjunto B e que ao mesmo tempo não pertençam ao A:
Já o conjunto I pede os elementos que pertencem ao conjunto A ou que pertençam ao U. Como o U tem todos os elementos, então na prática é a união de todo mundo:
Beleza? Vamos para o último?
Nosso último conjunto J pede todos os elementos que pertençam ao U e que não pertençam ao conjunto D, tudo isso ao mesmo tempo. Vamos relembrar do conjunto D:
Vemos que esses elementos estão dentro dos conjuntos A e B, então queremos os de fora! Apenas os que pertençam ao U mesmo, aqueles dois que estão por fora:
E é isso!
Espero ter ajudado! Vamos para a próxima?