UFSC – Pré Cálculo – Lista 2 – Questão 7a
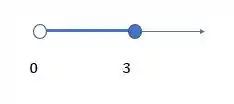
Dados os conjuntos e , efetuar as operações pedidas, dar as respostas na notação de intervalo e representar graficamente
Passo 1
E aí pessoal, tudo bem? O problema nos deu esses dois conjuntos aqui
e
E pediu para efetuar essa operação aqui e apresentar a resposta em formato de intervalo e também graficamente
Mas você lembra como fazer isso?
Quando temos de dois conjuntos estamos falando da operação de intersecção, isto é, queremos apenas os elementos que são comuns tanto ao conjunto A quanto ao conjunto B.
Então se temos um conjunto e outro , a intersecção deles serão apenas os elementos . E agora quando estamos falando de intervalos contínuos? Bom, se um elemento estiver incluso em um dos intervalos (por exemplo algum extremo que seja fechado) mas não estiver incluso em outro (com extremo aberto), então esse elemento não estará no conjunto intersecção!
A ideia para resolver essa questão é fazer um esquema dos conjuntos e verificar quais intervalos são comuns aos dois ao mesmo tempo
Beleza?
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Nossos conjuntos são
e
Graficamente temos:
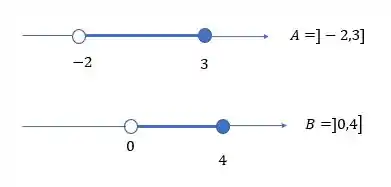
O conjunto intersecção será apenas os que existem no A e ao mesmo tempo no B
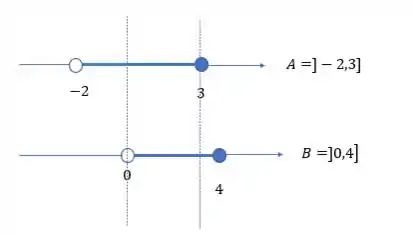
Tranquilo até aqui?
Notem que é o menor intervalo em comum! É aquele pedacinho no meio delimitado pelas retas pontilhadas. Agora vamos escrever esse resultado em formato de conjunto, lembrando que bolinha aberta no extremo significa que nosso resultado é aberto também
E de forma gráfica:
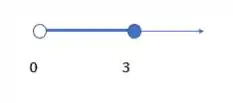
E é isso!
Espero ter ajudado! Vamos para a próxima?
Resposta
