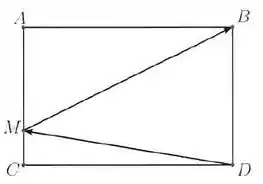
Considere a figura do retângulo abaixo. Sabendo que , escreva cada vetor a seguir como combinação linear de e .
a)
b)
Passo 1
a) Por soma de vetores, sabemos que
Beleza, mas queremos em função de e , então vamos achar uma relação.
Sabemos que , então:
Além disso, é de , logo:
Passo 2
b) Sabemos que
equivale a de :
Além disso, é congruente a , então podemos substituir:
Resposta
a)
b)
Exercícios de Livros Relacionados
Determine uma equação da esfera com centro em ( 2 , - 6 , 4 ) e raio 5 . Descreva sua intersecção com cada um dos planos coordenados.
Diz-se que o vetor v é combinação linear dos vetores v 1 ,v 2 ,...,v n quando se tem v=α 1 v 1+α 2 v 2+···+α n v n ,c o mα 1 ,α 2 ,...,α n∈R . Mostre que os vetores u ,vew são coplanares se, e somente
Determine uma equação da esfera com centro em ( 0 , 1 , - 1 ) e raio 4 . Qual é a intersecção dessa esfera com o plano y z ?
Escreva inequações para descrever a região dada.34. O cilindro sólido que está sobre ou abaixo do plano z = 8 e sobre ou acima do disco no plano x y com centro na origem e raio 2 .
Determine uma equação para o conjunto de pontos equidistantes dos pontos A ( - 1,5 , 3 ) e B ( 6,2 , - 2 ) . Descreva o conjunto.