Exercícios Resolvidos de Operações com Vetores

Exercício 10 1 2 3 4 5 6 7 8 9 11 12 13 14 15 16 17 18 19 20 21 22 23

Enunciado

USP, Álgebra Linear 1 – PREC – 2016 – Questão 13

Seja um triângulo no espaço e sejam um ponto do segmento e um ponto do segmento tais que:

Se é o ponto na interseção dos segmentos e , então o quociente

é igual a:

;

;

;

;

.

Passo 1

E aí, minha gente! Tudo bem? Antes de começarmos a resolver a questão propriamente dita, vamos esboçar as informações que o enunciado nos deu para ficar mais claro:

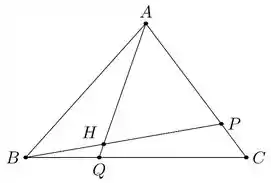
Agora que desenhamos o triângulo e os segmentos e , vamos tentar escrever expressões vetoriais para fazer uso da praticidade em se expressar a soma de vetores e também para que possamos utilizar as informações fornecidas no enunciado de que:

Primeiramente, vamos começar escrevendo as duas seguintes equações vetoriais:

Para entendermos de onde vêm as relações acima, é sempre bastante conveniente fazermos desenhos:

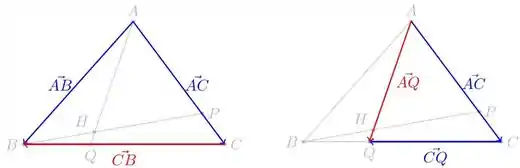
Beleza! Mas agora, do enunciado, sabemos que , certo? Mas como os pontos são colineares:

Então, no nosso sistema de duas equações, podemos substituir a relação acima na segunda equação:

Show! Finalmente, vamos substituir a primeira equação do nosso sistema na equação acima:

Vamos deixar essa nossa equaçãozinha guardada por ora, mas já já vamos utilizá-la. O que vamos fazer agora é encontrar outra relação desse tipo, de forma bastante análoga ao que acabamos de fazer. Se liga, vamos escrever um nova equação vetorial:

De novo, para gente se convencer dessas relações entre vetores, nada melhor do que um desenho haha:

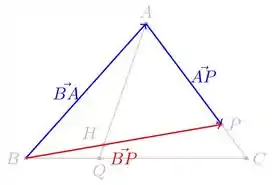
Show! Assim como fizemos antes, vamos usar a informação remanescente do enunciado: . Como os pontos e são colineares, temos:

Então, utilizando da equação acima na nossa nova relação entre vetores, obtemos:

Passo 2

Para resumir até onde chegamos por enquanto, obtivemos as duas seguintes equações vetoriais:

Agora, como os pontos são colineares e os pontos também, então

para algum , assim como tínhamos nas equações que relacionavam , e , . Dessa forma, podemos reescrever as duas equações vetoriais em função de e :

Antes de prosseguirmos ao próximo passo, é importante notarmos que como , o número é precisamente aquilo que estamos buscando como resposta da nossa questão, já que:

Passo 3

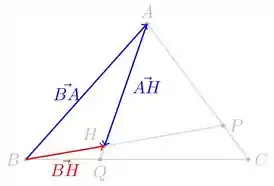
Beleza, temos duas equações que relacionam e com e , certo? Para finalizar precisamos de alguma última equação que nos permita juntar essas duas informações, ou seja, alguma equação que relacione com e com ou (ou ambos). Para esse propósito, vamos utilizar a seguinte equação:

Novamente, como uma imagem vale mais do que mil palavras, a relação acima está ilustrada na figura abaixo:

Substituindo então as equações que já temos para e , temos:

Rearranjando:

Agora, vamos pensar o seguinte: como os vetores são LI, uma combinação linear deles só teria como dar o vetor nulo se os coeficientes fossem zero, certo? Então podemos usar isso para montar um sisteminha de equações: