Sabendo que o ângulo entre os vetores e é de , determinar o ângulo formado pelos vetores:
- e
- e
- e
- e
Passo 1
O enunciado nos diz que o ângulo entre os vetores e é de . Então, temos que:
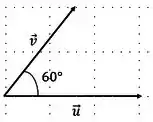
Queremos determinar,a gora, o ângulo entre diferentes vetores. Para isso, vamos utilizar o método das figuras, ou seja, vamos desenhar os vetores, para achar os ângulos.
- O primeiro ângulo, é entre os vetores e
- Próximo ângulo é entre e
- Ângulo entre os vetores e
- Ângulo entre e
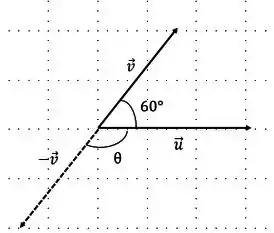
Passo 2
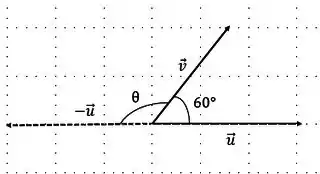
Passo 3
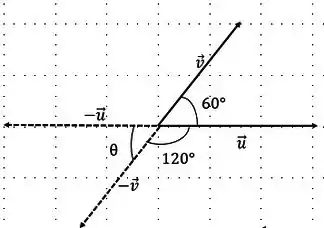
Passo 4
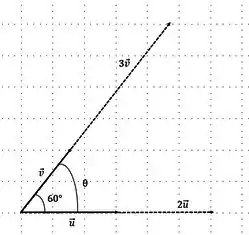
Resposta
- , b) , c) e d)
Exercícios de Livros Relacionados
Determine uma equação da esfera com centro em ( 2 , - 6 , 4 ) e raio 5 . Descreva sua intersecção com cada um dos planos coordenados.
Diz-se que o vetor v é combinação linear dos vetores v 1 ,v 2 ,...,v n quando se tem v=α 1 v 1+α 2 v 2+···+α n v n ,c o mα 1 ,α 2 ,...,α n∈R . Mostre que os vetores u ,vew são coplanares se, e somente
Determine uma equação da esfera com centro em ( 0 , 1 , - 1 ) e raio 4 . Qual é a intersecção dessa esfera com o plano y z ?
Escreva inequações para descrever a região dada.34. O cilindro sólido que está sobre ou abaixo do plano z = 8 e sobre ou acima do disco no plano x y com centro na origem e raio 2 .
Determine uma equação para o conjunto de pontos equidistantes dos pontos A ( - 1,5 , 3 ) e B ( 6,2 , - 2 ) . Descreva o conjunto.