UFPE – Geometria Analítica – 2018.2 – P1 – Questão 1
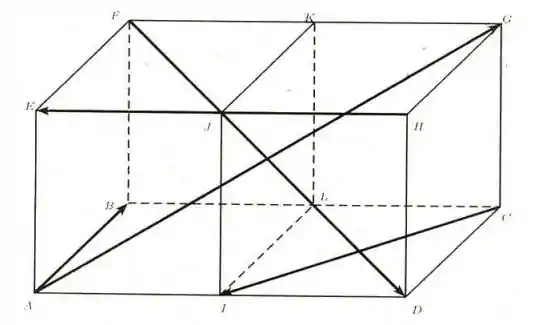
Na figura abaixo estão representados dois cubos unidos por uma face. Determine a soma dos vetores indicando um representante do resultado com os pontos da figura.
Passo 1
A primeira coisa que precisamos reparar é que e que . Isso é útil por causa do seguinte: olha como fica a soma!
Vamos reescrever isso numa ordem conveniente:
Passo 2
Qual foi a idéia de escrever assim? Tá vendo que o segundo ponto de um vetor é o primeiro ponto do vetor seguinte? Então isso aí vai ser um caminho que vamos seguindo. No final, o que importa é o começo e o fim da linha! Então essa soma toda vai virar:
Fechou! Gostou da idéia? Ela é muito útil pra resolvermos essas somas enormes.
Resposta
Exercícios de Livros Relacionados
Determine uma equação da esfera com centro em ( 2 , - 6 , 4 ) e raio 5 . Descreva sua intersecção com cada um dos planos coordenados.
Diz-se que o vetor v é combinação linear dos vetores v 1 ,v 2 ,...,v n quando se tem v=α 1 v 1+α 2 v 2+···+α n v n ,c o mα 1 ,α 2 ,...,α n∈R . Mostre que os vetores u ,vew são coplanares se, e somente
Determine uma equação da esfera com centro em ( 0 , 1 , - 1 ) e raio 4 . Qual é a intersecção dessa esfera com o plano y z ?
Escreva inequações para descrever a região dada.34. O cilindro sólido que está sobre ou abaixo do plano z = 8 e sobre ou acima do disco no plano x y com centro na origem e raio 2 .
Determine uma equação para o conjunto de pontos equidistantes dos pontos A ( - 1,5 , 3 ) e B ( 6,2 , - 2 ) . Descreva o conjunto.