Dados os vetores e da figura, mostrar, num gráfico, um representante do vetor:
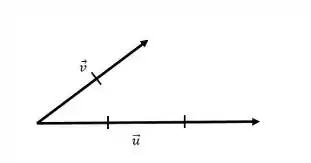
Passo 1
O exercício nos deu o desenho dos dois vetores que devemos considerar. Com esse desenho devemos realizar operações entre vetores. Aqui, como foi nos pedido devemos desenhar os vetores.
Passo 2
- Temos que achar o vetor que é
- Agora, o vetor a ser encontrado é
- Próximo vetor:
- Desenhar
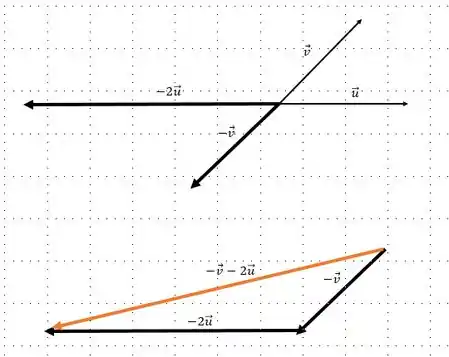
Para resolver esse item, temos que lembrar que , ou seja, o vetor no sentido oposto.
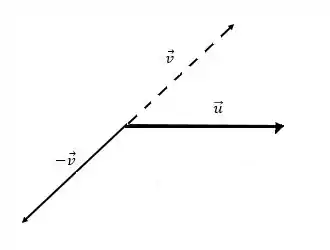
Podemos também transladar o vetor sem mudar o módulo, e sentido do vetor:
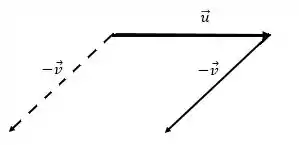
Dessa forma, podemos fazer a soma de vetores:
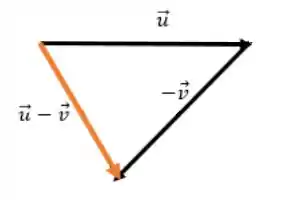
Prontinho, conseguimos o vetor , seguimos os seguintes passos:
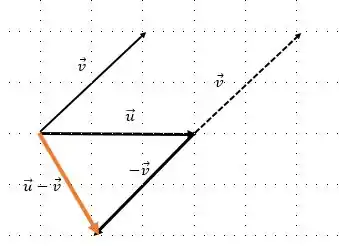
Passo 3
Da mesma forma do item (a), vamos transladar o vetor e encontrar o vetor :
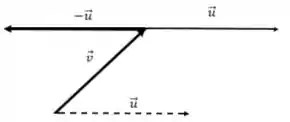
Agora podemos encontrar a soma de vetores:
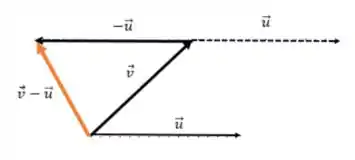
Passo 4
Primeiro vamos encontrar o vetor e :
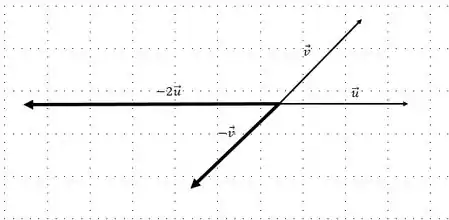
Agora podemos encontrar a soma de vetores:
Passo 5
Até então, estávamos usando a proporção dos quadrados , mas como a figura ficaria muito grande fizemos que quadriculado equivale a .
Primeiro, vamos encontrar os vetores para soma :
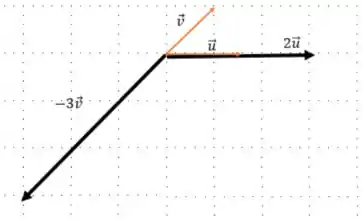
Podemos transladar o vetor para a esquerda para podermos encontrar a soma mais facilmente:
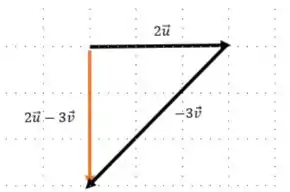
Show de bola?!
Resposta
Ei, a resposta está no passo a passo :)