USP – Álgebra Linear – P1 2020 – Questão 6
Considere o tetraedro de vértices . Seja o ponto sobre a aresta tal que e seja o ponto sobre a aresta tal que . Se são tais que , então são iguais, respectivamente, a
Passo 1
OIEE! Vamos lá matar mais um?
Temos esse tetraedro:
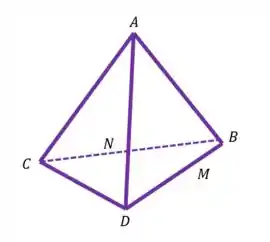
Onde e
E aí queremos encontrar uma relação de com , e , tipo assim:
E então encontrarmos os valores de
O nosso ponto de partida para chegarmos nessa relação é que
Pode ser? Então vamos desenvolver isso aí!
Passo 2
Então temos
Mas
Também sabemos que , então
Decompondo os vetores na soma de 2 vetores envolvendo o ponto :
Como queremos uma relação que envolva , e , vamos manipulando isso
Passo 3
Temos que
Mas , então
Aeeee, então chegamos em algo do tipo
E aí, comparando, temos que
Sucesso!
Resposta
Exercícios de Livros Relacionados
Determine uma equação da esfera com centro em ( 2 , - 6 , 4 ) e raio 5 . Descreva sua intersecção com cada um dos planos coordenados.
Diz-se que o vetor v é combinação linear dos vetores v 1 ,v 2 ,...,v n quando se tem v=α 1 v 1+α 2 v 2+···+α n v n ,c o mα 1 ,α 2 ,...,α n∈R . Mostre que os vetores u ,vew são coplanares se, e somente
Determine uma equação da esfera com centro em ( 0 , 1 , - 1 ) e raio 4 . Qual é a intersecção dessa esfera com o plano y z ?
Escreva inequações para descrever a região dada.34. O cilindro sólido que está sobre ou abaixo do plano z = 8 e sobre ou acima do disco no plano x y com centro na origem e raio 2 .
Determine uma equação para o conjunto de pontos equidistantes dos pontos A ( - 1,5 , 3 ) e B ( 6,2 , - 2 ) . Descreva o conjunto.