UTFPR, Sem Campus, Física 1, Listas de Física 1 - UTFPR - Lista 1 - Sistemas de unidades e Análise Dimensional e Vetores, Questão 16
16) Determine as componentes e dos seguintes vetores que estão no plano .
a) Vetor deslocamento de que forma um ângulo de no sentido horário a partir do eixo .
b) Vetor velocidade de que forma um ângulo de no sentido anti-horário com o eixo .
c) Força de que forma um ângulo de no sentido anti-horário com o eixo .
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema temos alguns vetores que foi dado em modulo e o ângulo que o vetor faz com algum eixo de referência.
Como podemos fazer isso? 🤔🤔
O modulo de um vetor pode ser chamado como o tamanho do vetor e a partir do ângulo que esse vetor faz com a referência dada, podemos obter as componentes desse vetor a partir das relações trigonométricas do e .
Sacou, bora começar!
Passo 2
O primeiro vetor é um vetor deslocamento, tem modulo de e faz um ângulo de no sentido horário a partir do semieixo positivo de . Ou seja
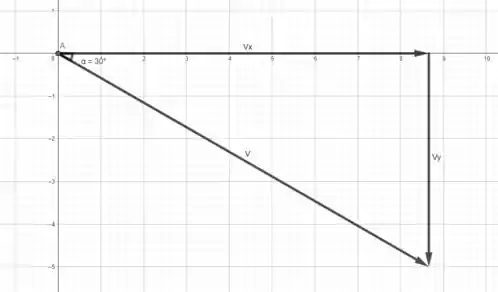
Como o cosseno é igual a razão entre o cateto adjacente e a hipotenusa, então
Como é o modulo do vetor, então
E como o seno é igual a razão entre o cateto oposto e a hipotenusa...
Mas como aponta para baixo, quando passarmos para o vetor , ele deverá ter valor negativo.
Como , então
Entendeu essa parte? 👀
Passo 3
Agora foi dado um vetor velocidade de modulo e que faz um ângulo de no sentido anti-horário com o semieixo negativo de . Ou seja
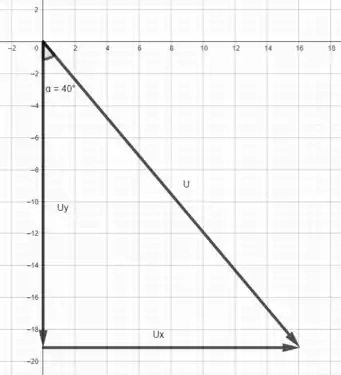
Fazendo a mesma análise de cosseno e seno que fizemos anteriormente, temos para a componente do vetor
E para a componente
Mas como aponta para baixo, ele deve ser negativo
Escrevendo o vetor , temos
Bacana, não é? 😁
Passo 4
Por último, foi dado um vetor força de que forma um ângulo de no sentido anti-horário com o semieixo negativo de . Ou seja
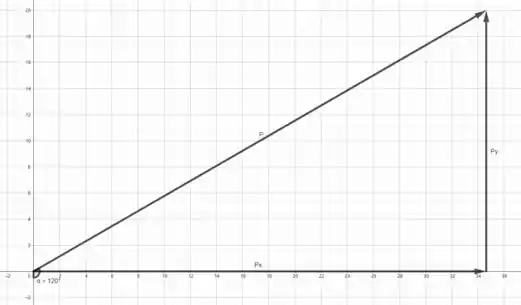
Se o ângulo entre o semieixo negativo de com o vetor é de e o ângulo entre o semieixo negativo de com o semieixo positivo de é , o ângulo que podemos usar nas nossas análises é o ângulo entre o semieixo positivo de e o vetor
Para obter , temos
Para obter , fazemos
Escrevendo o vetor sabendo que ambos os componentes apontam para os semieixos positivos, temos
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
a)
b)
c)