UFMG; Fundamentos de mecânica; Provas – P1; 2022.1; Questão P2.2
Considere o sistema da figura ao lado. O bloco de forma triangular possui massa e o que está sobre ele, . A rampa do bloco de baixo faz um ângulo com a horizontal. O coeficiente de atrito cinético entre o bloco de massa M e a superfície do piso é . Existe atrito entre os dois blocos, de coeficiente (estático igual ao cinético), mas este é pequeno e insuficiente para manter o bloco de massa m parado sobre o de baixo, se o de baixo estiver parado. Uma força F é aplicada sobre o bloco de baixo, como na figura, para acelerá-lo de tal forma, que o bloco de cima não deslize sobre o de baixo, enquanto o conjunto se movimenta sobre o piso. Uma força F é feita de forma que o conjunto se movimente sobre o piso, mas o bloco de cima continue sem se movimentar sobre o de baixo, com a força de atrito estático entre os blocos estando em seu limite máximo (o bloco de cima está na iminência de começar a DESCER sobre o de baixo). Dê suas respostas em termos de .
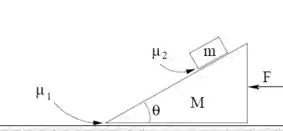
P2.2 – Calcule o valor da normal entre os blocos nessa situação.
Passo 1
Faaaala galera! Tudo certinho com vocês?? Bora lá resolver mais um probleminha!
A gente pode responder essa questão em poucos passos, então me acompanha!!!
Por uma análise no enunciado do nosso problema, sabemos que o bloco de massa se movimenta apenas na horizontal, sem que suba ou desça sob o bloco de massa , dessa forma, podemos afirmar que a sua força de aceleração na vertical é nula. Pelo sistema de coordenadas da figura abaixo, podemos escrever:
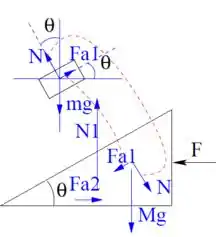
Se liga que o enunciado do problema nos diz para calcular o valor da normal na situação limite, quando o bloco menor está na iminência de descer sobre o maior. Nesse caso, a força de atrito aponta para cima da rampa de e seu valor vale . Substituindo esse valor na equação anterior, temos:
Colocando em evidencia, temos:
E tá aí nossa resposta, te ajudei?? Então te vejo na próxima!
