Um bloco de massa está sobre o solo, quando passa atuar sobre ele uma força de módulo que faz um ângulo com a horizontal, conforme mostra a figura. Os coeficientes de atrito estático e cinético entre o bloco e o solo são e respectivamente. Utilize .
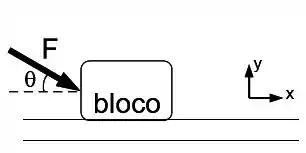
a) Que tipo de força de atrito age sobre o bloco? Determine esta força. Utilize o sistema de coordenadas indicado na figura e seus respectivos vetores unitários para a sua resposta.
Agora o mesmo bloco é agora colocado sobre uma prancha de massa e ambos são colocados sobre uma mesa com atrito desprezível. A mesa não é mostrada na figura. O coeficiente de atrito estático entre o bloco e a prancha é . O sistema entra em movimento quando uma força horizontal de módulo atua sobre a prancha conforme mostra a figura. Não há movimento relativo entre o bloco e a prancha.
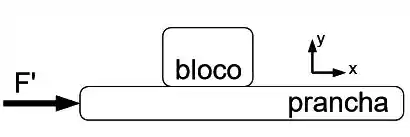
b) Faça um diagrama de corpo livre para o bloco e para a prancha. Indique de forma clara nos diagramas que forças constituem pares ação-reação.
c) Escreva as equações de movimento em termos das suas componentes para o bloco e para a prancha. Utilize o sistema de coordenadas indicado na figura.
d) Calcule o valor máximo de para que não haja movimento relativo entre o bloco e a prancha. Calcule a aceleração do conjunto para este caso.
Passo 1
(a)
Do diagrama do corpo livre do bloco, as equações de movimento em termos de componentes são:
Eixo :
Eixo :
O corpo se moverá somente se:
Logo como é maior que a força de atrito estático máxima, o corpo irá conseguir se mover e sobre este age atrito cinético, dado por:
Passo 2
(b)
As forças de atrito entre o bloco e a prancha são pares ação e reação, além da força normal de contato entre o bloco e a prancha.
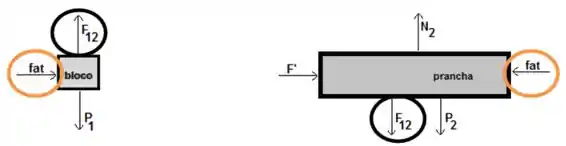
Passo 3
(c)
Utilizando a segunda lei de Newton:
Para o bloco:
Eixo :
Eixo :
Para a prancha:
Eixo :
Eixo :
Passo 4
(d)
Utilizando as seguintes equações do item anterior:
Para o bloco:
Eixo :
Para a prancha:
Eixo :
Não havendo movimento relativo entre os blocos, estes se movem juntos e . O valor máximo da força será alcançado quando o bloco estiver na iminência de escorregar em relação à prancha, ou seja, quando a força de atrito estática for máxima. Nesta situação temos:
Logo:
Substituindo o valor obtido na equação da prancha:
Resposta
(a) Força de atrito cinética:
(b) 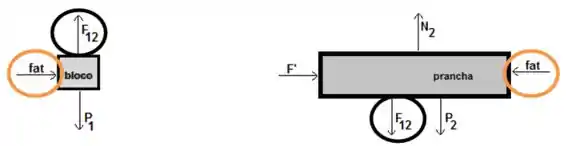
(c)
(d)