Uma pessoa de massa tenta puxar uma caixa de massa sobre uma superfície inclinada, através de uma corda e uma polia ideais, de acordo com a figura abaixo. A superfície inclinada define um ângulo com a horizontal, e a pessoa encontra-se no topo, em uma superfície horizontal. O coeficiente de atrito estático entre a caixa e a superfície é e o coeficiente de atrito estático entre o sapato da pessoa e a superfície é .
(a) Desenhe na figura todas as forças exercidas na pessoa e na caixa.
(b) Encontre o valor mínimo de para que a pessoa consiga mover a caixa. Verifique seu resultado para o limite para e
(c) Substituindo os valores de , , , e , encontre o mínimo valor de para que seja possível mover a caixa. Utilize a aproximação e .
(d) O que você deverá mudar em seus cálculos se a pessoa também estiver no plano inclinado? Recalcule o resultado do item anterior para este caso.
Passo 1
(a) Ver as forças que atuam no nosso sistema:
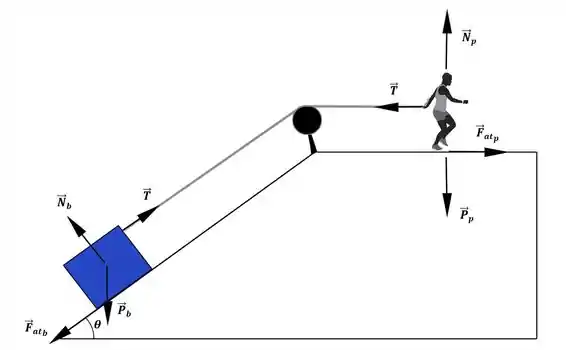
Como nem a pessoa nem o bloco estão no espaço, ambos vão ter força peso apontando pra baixo, beleza? Temos ainda a tração da corda, que sempre tem a mesma intensidade nas duas pontas se for inextensível.
E essas forças de atrito aí, porque estão assim? Bem, lembra que a força de atrito se opõe à tendência de movimento? Como, se a pessoa não fizer força nenhuma na corda, o bloco tende a puxar ela, a força de atrito pra pessoa é da esquerda pra direita e como se a pessoa puxar a corda o bloco tende a subir, a força de atrito pro bloco “aponta” no sentido da descida do bloco, ok?
Pra ficar mais organizado, vamos decompor a força peso. No esquema anterior, vamos olhar só pra parte triangular. Dá uma olhada em como fica:
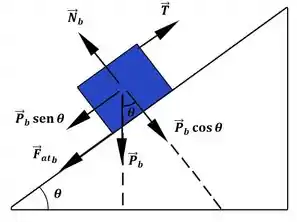
Agora que decompomos a força peso podemos redesenhar nossos diagramas de corpo livre:
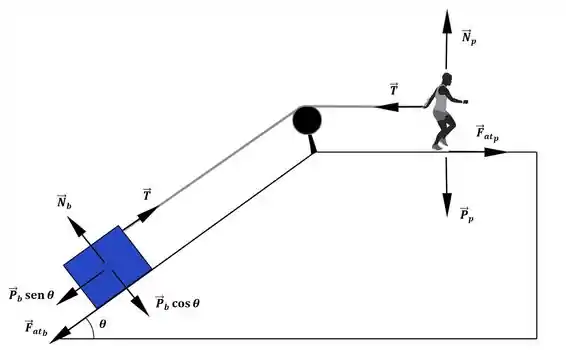
Passo 2
(b) Verificar as condições para que o bloco se mova
Vamos lá, a gente quer que o bloco se mova, certo? Então pro bloco subir vamos ter que puxar a corda! Quando puxamos a corda, garantimos que:
Calma, parece estranha essa forma de escrever, não é mesmo? Mas isso só porque não substituímos as expressões acima por valores conhecidos. Pro peso, vamos ter:
Mas agora, e essa força de atrito ai? O que fazemos com ela? Se o bloco estiver na iminência de se mover, essa força de atrito tem que ser seu valor máximo. Se não fosse, a pessoinha ali em cima não puxou a corda forte o suficiente pra vencer o atrito estático. Então:
Mas como decompomos já a força peso, então já sabemos com quem a normal do bloco se iguala:
E agora, substituindo na expressão da fórmula de atrito:
E botando tudo junto, temos:
Passo 3
E a pessoa lá em cima, o que acontece com ela?
No passo anterior, faltou uma coisa: descobrir quem é nosso misterioso . Bem, como queremos que o bloco suba, a pessoa não pode estar nem parada e nem se deixando levar pelo peso do bloco.
Pra pessoa no lá em cima, também vamos ter um valor máximo da força de atrito. Essa força vai ser:
Aqui não tem pegadinha com ângulo, podemos igualar a normal direto com o peso:
Agora, pensa aqui comigo. Se for muito pequeno, a ponto de ser menor que , a pessoa não se move e logo o bloco não se move. Se for muito grande, a ponto de ultrapassar , a pessoa vai se mover pro lugar errado e o bloco vai descer! Então pro bloco realmente subir, vamos ter que:
E aí conseguimos descobrir quem era o misterioso . Agora é só substituir:
Passo 4
Analisar os casos limite
O que vai acontecer se os ângulos tenderem pra e ? Vamos ver? Pra começar, vamos lembrar o seno e o cosseno desses dois ângulos limites:
Se o ângulo tender então para , vamos ter que:
Se o ângulo tender então para , a gente acha:
Ou seja, a força de atrito na pessoa deve ser maior que na caixa para o caso e para o caso , deve ser maior que o peso da caixa.
Passo 5
(c) Substituindo pelos valores do enunciado
Ainda não descobrimos o valor mínimo do coeficiente de atrito pro bloco. Ué, como assim? Calma, só não descobrimos meeeesmo porque não usamos números. Se:
Então agora só precisamos substituir mesmo:
Passo 6
(d) E se a pessoa tivesse no plano inclinado?
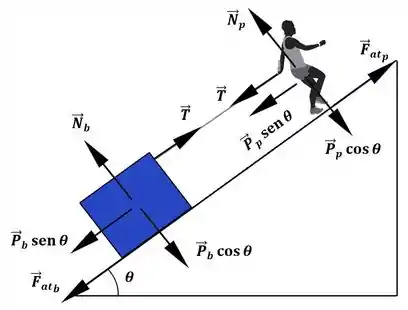
Se a pessoa tivesse no plano inclinado, aquela decomposição que fizemos pro peso do bloco seria feita da mesma forma pro peso da pessoa, não é mesmo? E, ainda, dá uma olhada na normal da pessoa: não é mais a mesma! Então como a posição da pessoa só que mudou, só o resultado dela vai mudar, ok? O resultado que vimos pro bloco a gente vai deixar quieto:
Mas agora não vale mais porque tem uma componente do peso na mesma direção e sentido de . Então:
Como a normal da pessoa se iguala com uma componente da força peso, temos:
E logo, conseguimos nossa expressão pra :
E olha lá! Duas expressões que envolvem ! Se juntarmos as duas então ficamos com:
E pra finalizar com chave de ouro, usando os dados da questão anterior, achamos um número pra esse coeficiente de atrito estático:
Resposta
(b)
(c)
(d)