No problema da questão (6), qual é a maior inclinação max da rua para que a carga não deslize na carroceria? Considere ainda que o caminhão se movimente com velocidade constante.

(A) max = arccos(µe)

(B) max = arcsen(µc)

(C) max = arcsen(µe)

(D) max = arctan(µc)

(E) max = arctan(µe)

Temos a seguinte situação no problema:

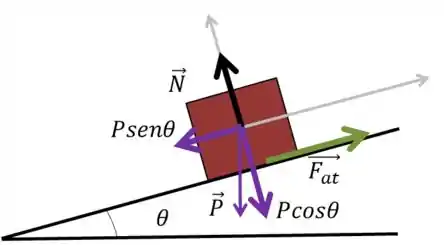
No problema anterior, achamos que:

O fato de o corpo está na iminência de deslizar, ou seja, na iminência do movimento implica de a estar no seu valor máximo, portanto:

Juntando essas duas últimas informações, temos que:

Como sabemos o valor da Normal

Podemos substituir aqui:

Como queremos encontrar o valor de para essa situação:

E assim achamos o ângulo crítico do plano inclinado. Isso quer dizer que, se aumentarmos o ângulo que o plano inclinado faz com a horizontal, de tal forma que sua tangente seja maior que o coeficiente de atrito estático do plano com o bloco, este bloco iniciará o movimento de descida.