Uma força horizontal , de módulo 40 N, empurra um bloco de peso 30 N contra uma parede vertical. O coeficiente de atrito estático entre a parede e bloco é 0,80 e o de atrito cinético é 0,60. Suponha que inicialmente o bloco esteja em repouso. A sentença correta é
(a) O bloco começará a se mover e o módulo da força resultante exercida pela parede sobre o bloco vale 32 N;
(b) O bloco começará a se mover e o módulo da força resultante exercida pela parede sobre o bloco vale 51,2 N;
(c) O bloco não se moverá e o módulo da força resultante exercida pela parede sobre o bloco vale 70 N;
(d) O bloco não se moverá e o módulo da força resultante exercida pela parede sobre o bloco vale 50 N;
(e) O bloco não se moverá e o módulo da força resultante exercida pela parede sobre o bloco vale 30 N;
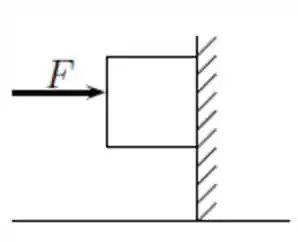
Passo 1
Vamos ver todas as forças que atuam no bloco quando ele está em repouso.
Tem a força , a força peso , e as forças exercidas pela parede, que são a normal e a força de atrito estático .
Então o diagrama de corpo livre do bloco é:
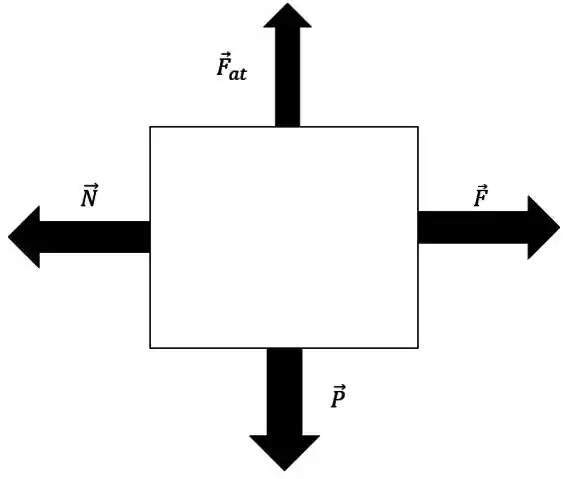
Passo 2
O bloco está em repouso, então a força resultante atuando nele é nula. Então também podemos dizer que a força resultante atuando no eixo também é nula:
E as forças agindo no eixo são a e a normal , logo:
Vou botar o módulo da normal como em vez de pra não confundir com Newton, ok?
Então ficou:
E ele deu , então
(Seria chato ficar né? rs)
Passo 3
Vamos fazer a mesma coisa no eixo . A força resultante é:
E como o bloco está em repouso:
Ou seja,
E o módulo da força peso vale , ou seja:
Passo 4
A força de atrito estático a gente só sabe calcular quando ela é máxima, quando o corpo está prestes a se mover. Então vamos assumir que o bloco está na iminência de um movimento, pra ver se a força de atrito da parede daria conta de manter o bloco em repouso.
A força de atrito estático máximo tem seu módulo dado por:
sendo o coeficiente de atrito estático. E aqui , logo:
E vimos que , então
Passo 5
Ou seja, se o bloco estivesse na iminência de um movimento, no ponto de cair, a força de atrito valeria . Ou seja, ela teria módulo maior que o do peso (), e manteria o bloco em repouso.
A força de atrito tem módulo : essa diferença de em relação à força de atrito estático máximo mostra que além do bloco não cair, nem quase caindo ele está.
Passo 6
Ainda falta definir a segunda parte da questão, da força resultante exercida pela parede sobre o bloco.
Essa força nada mais é que a soma da normal e da força de atrito. Mas não podemos simplesmente somar os módulos das forças, temos que somar os vetores!
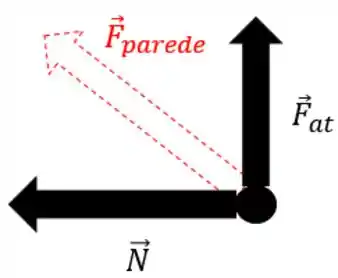
Passo 7
Sabemos que e , então pra achar só precisamos aplicar um Pitágoras básico:
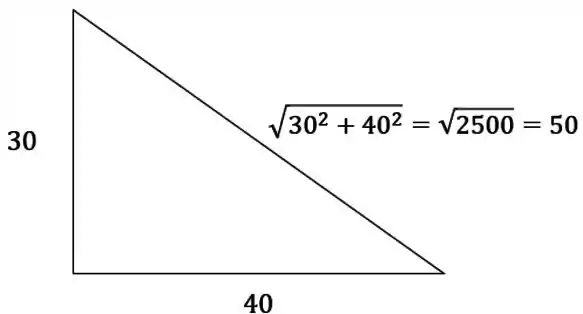
Ou seja, !
Resposta
Alternativa (d)