Fundamentos de Fisica - Vol. 1. Halliday - 8ª Edição, Capítulo 6 – seção 3 - Problema 23.
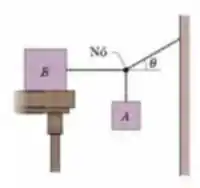
(Cap 6 – Ex 23) O bloco da Fig. 6-31 pesa . O coeficiente de atrito estático entre o bloco e a mesa é ; o ângulo é ; suponha que trecho da corda entre o bloco e o nó é horizontal. Determine o peso máximo do bloco para o qual o sistema permanece em repouso.
Passo 1
Faaaaaalaiiii, tudo na boaaa?
Para iniciar vamos fazer o diagrama de corpo livre para os dois blocos e também para o nó. Primeiro expressando as forças que atuam sobre o bloco , temos:
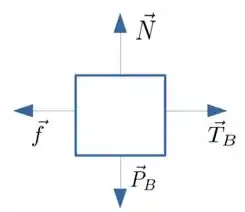
Agora sobre o nó:
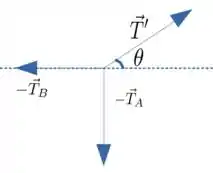
E também para o bloco , obtemos:
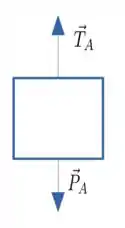
Para resolver este problema temos que ter em mente a relação da força de atrito estático máximo:
Passo 2
Aplicando a segunda lei de Newton para o bloco no eixo , vemos que:
Como o enunciado pede o valor de máximo para não entrar em movimento, então podemos considerar , afinal, se houvesse aceleração, o corpo entraria em movimento. Logo:
Isolando :
Passo 3
Belejóia meu aprovado, de maneira análoga, podemos afirmar que o nó está em equilíbrio, portanto, em cada eixo:
E como no eixo obtemos a igualdade:
Isolando :
Agora, substituindo essa informação, no eixo :
Passo 4
Agora aplicando a segunda lei de Newton para o bloco no eixo :
Como queremos que o bloco permaneça em repouso, então . Assim:
E já que , então:
Isolando :
Passo 5
Então para determinar o valor da massa de , precisamos agora determinar o valor da força normal . Para tanto, aplicaremos a segunda lei de Newton para o eixo :
Como não há movimento, . Assim:
Isolando :
Passo 6
Por fim, voltando pra nossa equação da massa:
Substituindo os valores dado pelo enunciado:
E, portanto, o peso de é:
