UFRJ, Sem Campus, Física 1, Listas de F1 - Engenharias UFRJ Macaé - 3ª Lista - Dinâmica - Leis de Newton, Questão 4a
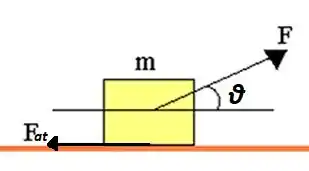
Um bloco de massa está sobre uma mesa horizontal, como mostrado na figura. O bloco é puxado por uma corda sem massa com uma força a um ângulo . O coeficiente de atrito estático . O valor mínimo da força necessária para mover o bloco depende do ângulo . Mostre que
- a expressão para o módulo da força em função do ângulo é dada por .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um bloco de massa sendo arrastado por uma mesa horizontal através de uma força , veja:
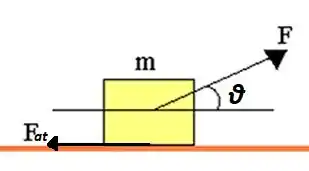
Onde é a força de atrito.
Dessa forma, a questão nos diz para provar que a expressão para o módulo da força em função do ângulo é dada por .
Para determinarmos , devemos decompor as forças em e para analisarmos melhor o movimento.
Lembrando que temos que encontrar o nosso valor de na iminência do movimento, quando ainda.
E aí? Bora lá?
😉
Passo 2
Então... Vamos aplicar a 2ª Lei de Newton no eixo :
Vamos considerar que a força de atrito estático é máxima, ou seja, o bloco está na iminência de se movimentar:
Agora, decompondo no eixo :
Passo 3
Agora, substituindo , temos:
Entendeu direitinho? Responde aee ;)
