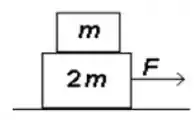
Uma caixa de massa é colocada em cima de uma caixa maior de massa como mostrado na figura. Quando uma força de módulo é aplicada na caixa grande, ambas as caixas se movem para a direita com a mesma aceleração. Supondo que o coeficiente de atrito entre as caixas é e que não há atrito entre a caixa maior e ochão, qual é a força atuando na massa menor?
Passo 1
Bom galera, vamos analisar o sistema devagar.
A primeira informação importante é que as massas se movem juntas e com a mesma aceleração.
E como não há um atrito no chão com a caixa maior, a força de atrito existente funciona como uma força interna, algo que mantem as duas caixas unidas.
Por isso, podemos usar logo a segunda lei de Newton e determinar a aceleração do conjunto:
Beleza?
Toda vez que te disserem (“ tal conjunto se move junto”) você pode tratar esse conjunto como um único corpo de massa cujo valor é a soma de todas as massas.
Passo 2
Beleza, mas você também pode analisar as partes individualmente. Uma pergunta que você precisa se fazer aqui é: Que força atua na massa
Bom, só tem a força de atrito( to falando das forças horizontais, porque tem sim o peso e a normal), já que a força não atinge a massa
Assim, podemos dizer que:
Só que já sabemos
Acabou (:
e)
Resposta
e)