Dois blocos, e , realizam um movimento retilíneo com aceleração constante. Uma força constante de módulo igual a atua sobre o bloco . O bloco está em repouso em relação ao bloco , lateralmente apoiado a esse como mostra a figura. O coeficiente de atrito estático entre os blocos e vale . Não há atrito entre o bloco e o solo. As massas dos blocos e valem respectivamente, e . Considerando a aceleração da gravidade igual a :
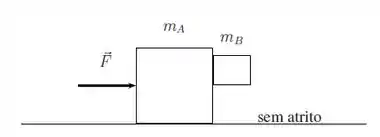
a) Faça o diagrama das forças que atuam sobre cada um dos blocos.
b) Qual o módulo da aceleração dos blocos? Justifique sua resposta.
c) Determine o módulo de todas as forças que atuam sobre o bloco .
d) Qual o menor valor que o módulo da força que atua sobre o bloco deve ter para que o bloco não deslize sobre a superfície do bloco ?
Passo 1
Nessa questão, temos uma força atuando sobre o bloco . O bloco , por sua vez acaba empurrando o bloco , através de uma força normal.
Já que o bloco tende a cair com a força peso e ele tem uma força normal na superfície de contato, vai aparecer uma força de atrito que tenta manter o bloco parado. Como ele está em repouso com relação a , temos que é suficiente para evitar que o bloco caia (deslize para baixo).
Então vamos aos itens.
Passo 2
a) Faça o diagrama das forças que atuam sobre cada um dos blocos.
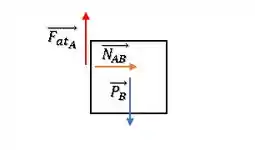
Vamos começar por . Ele terá uma força peso () apontando para baixo, uma força normal que o bloco exerce em () , ou seja, o bloco empurra o bloco . Além disso temos uma força de atrito exercida pelo bloco () que aponta contra a tendência de cair do bloco , logo, aponta para cima.
O diagrama de forças no bloco vai ser assim:
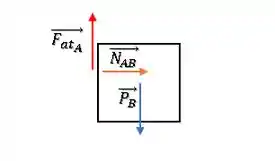
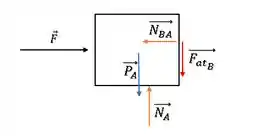
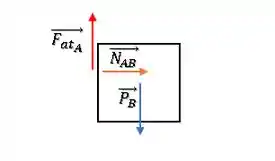
Agora, vamos ao bloco . Temos sua força peso () para baixo, a força () para a direita, a força normal de contato com o solo () para cima. Além disso, se ele empurra o bloco , pela ação e reação, o bloco empurra de volta com a mesma força, que chamaremos como a normal de em (). Por último, temos também a reação da força de atrito (), se o bloco tende a cair, ele tenta arrastar o bloco para baixo, então esse atrito aponta para baixo (contrário de ).
O diagrama de forças no bloco será assim:
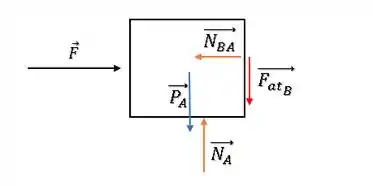
Passo 3
b) Qual o módulo da aceleração dos blocos? Justifique sua resposta.
Os dois blocos andam com a mesma aceleração. Podemos considerar os dois como um blocão com a massa equivalente à soma das massas dos dois blocos ():
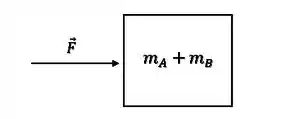
Temos que as forças internas sempre se cancelam, como por exemplo com , por isso quando juntamos os blocos, elas somem.
Das forças externas a única que está atuando na horizontal é a força que está no desenho, então aplicamos a segunda lei de Newton:
Passo 4
c) Determine o módulo de todas as forças que atuam sobre o bloco .
Começamos com a força , temos que a massa , então seu módulo é:
Agora podemos fazer o somatório de forças na vertical. Como ele está em repouso com relação à , ele não se move na vertical, então o somatório de forças é nulo:
Por último, podemos descobrir o módulo de a partir da segunda lei de Newton, pois temos a massa e sabemos sua aceleração ():
Passo 5
d) Qual o menor valor que o módulo da força que atua sobre o bloco deve ter para que o bloco não deslize sobre a superfície do bloco ?
Agora, vamos considerar a situação limite, onde o bloco está prestes a deslizar, então a força será a menor força possível que seja suficiente para evitar que o bloco caia.
Numa situação limite, onde uma determinada força normal () atua sobre o bloco , a força será a força de atrito estático máxima dada por:
Então, como a força de atrito () se anula com à força peso ():
A ideia agora vai ser relacionar os blocos e . Podemos fazer isso a partir da aceleração, que é a mesma para os dois.
Então vamos achar a aceleração com o bloco e depois usar isso para encontrar a força () em .
Então, vamos lá. Em
Já achamos que :
Com a aceleração, podemos aplicar a segunda lei de Newton para o bloco :
A força é reação de , logo elas têm o mesmo módulo que já encontramos anteriormente:
Substituindo e , conseguimos encontrar :
Resposta
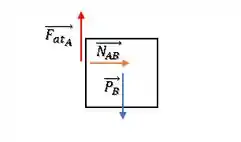
(a) Bloco :
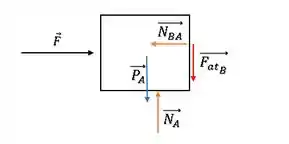
Bloco :
(b)
(c) ; ;
(d)