Três blocos de massa , e estão dispostos como visto na figura abaixo. Atua no bloco de massa uma força externa , horizontal e de módulo que faz o conjunto de blocos se movimentar. O bloco de massa não escorrega sobre o bloco de devido ao atrito estático atuando na interface entre estes dois blocos. Não existe atrito entre os blocos de massa e com o solo. Considerando a aceleração da gravidade determine:
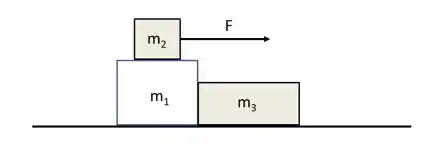
Os diagramas das forças que atuam em cada um dos três blocos;
A aceleração do bloco de massa ;
A força que o bloco de massa faz no bloco de massa ;
O coeficiente de atrito estático entre os blocos de massas e .
Passo 1
Vamos começar fazendo o diagrama de forças, o famoso diagrama do corpo livre DCL.
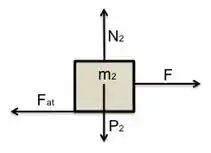
No bloco de massa , atuam:
- Força peso
- Força normal, que o bloco de massa faz sobre ele
- Força externa
- Força de atrito estático entre ele e o bloco de massa
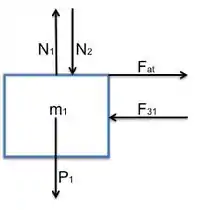
No bloco de massa , atuam:
- Força peso
- Força normal, que o plano faz sobre ele
- Força de contato entre ele e o bloco de massa
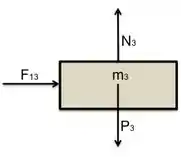
No bloco de massa , atuam:
- Força peso
- Força normal que o plano exerce sobre ele
- Força normal que o bloco de massa exerce sobre ele
- Força de atrito estático entre ele e o bloco de massa
- Força de contato entre ele e o bloco de massa
Passo 2
Agora que já conhecemos as forças e como elas atuam, podemos montar as equações de movimento para cada bloco. Como existe um vínculo entre os blocos, a aceleração de todos será a mesma.
Para o bloco de massa , temos:
Para o bloco de massa , temos:
Para o bloco de massa , temos:
Somando todas as equações, temos:
Repare que e tem o mesmo módulo, pois são um par de ação e reação! Por isso pudemos cancelar, do mesmo modo que cancelamos a força de atrito.
Isolando a aceleração, temos:
Substituindo, temos:
Passo 3
Agora que sabemos a aceleração, para determinar a força que o bloco de massa faz no bloco de massa , basta olhar para a equação de movimento do boco de massa , pois sabemos que temos:
substituindo os valores, temos:
A direção e o sentido estão descritos no diagrama do corpo livre que fizemos no item .
Passo 4
Para determinar o coeficiente de atrito estático, precisamos retomar a equação de movimento do bloco de massa , temos então:
Onde a
Substituindo os valores conhecidos, temos:
Resposta
Ver figuras acima