USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e e Energia, Questão 42a
Uma vagão pode deslizar, sem atrito, sobre uma superfície horizontal. Um bloco , de massa , está encostado na face vertical do bagão, como mostra a figura . O coeficiente de atrito entre o bloco e o vagão é .
Determinar a aceleração mínima do vagão para que o bloco não caia;
Passo 1
Eaew, tudo certinho com você?
O enunciado descreve a situação representada por
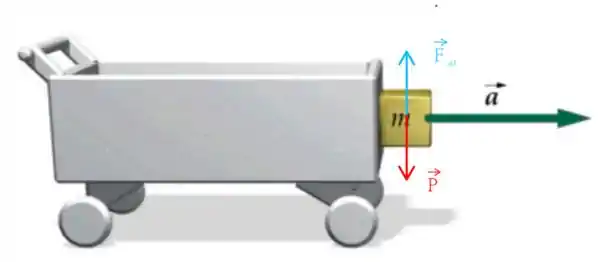
em que o carrinho se move sem sofrer atrito devido ao chão. No entanto, a força de atrito impede a massa de cair devido a seu peso . O coeficiente de atrito entre o bloco e o carrinho é . A alternativa nos pede para obter
Determinar a aceleração mínima do vagão para que o bloco não caia;
Qual será a aceleração mínima? Para que o bloco não caia, temos que verticalmente o movimento deve estar em equilíbrio, ou seja, temos que
A partir daqui podemos resolver o nosso problema! Só vamos precisar lembrar qual a definição de força de atrito estática! Saca só!
Passo 2
A força de atrito estática é tal que
e a força peso é tal que
Ou seja, a aceleração mínima será obtida quando o módulo da força normal for tal que
Mas como relacionamos isso a aceleração do carrinho?
Passo 3
Note que a força normal surge uma vez que a aceleração do carrinho pressiona o bloco contra a superfície de sua frente! Sendo assim, podemos igualar a força normal à
Como o módulo que achamos no passo anterior era para o equilíbrio, temos que
ou simplesmente
A primeira alternativa foi isso! Te vejo na próxima! Tchau Tchau!