UFABC – Fenômenos Mecânicos – Lista 3 – Questão 06
Um caixote de é arrastado sobre um piso, puxado por uma corda inclinada acima da horizontal. (a) Se o coeficiente de atrito estático é , qual é o valor mínimo do módulo da força para que o caixote comece a se mover? (b) Se , qual é o módulo da aceleração inicial do caixote?
Passo 1
Oi pessoal, essa questão parece complicada, mas vou ajudar você aqui!
Primeiro vamos fazer um desenho esquemático do que está acontecendo: temos um caixote sendo puxado por uma corda que está inclinada em acima da horizontal. Há atrito entre a caixa e a mesa, então podemos esquematizar assim nosso problema:
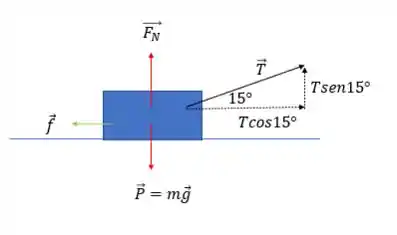
Como de costume escolhemos um eixo horizontal para a direita e um eixo vertical para cima. Supomos que o caixote está inicialmente em repouso.
A ideia é aplicar a segunda lei de Newton e determinar a força que precisamos aplicar na corda para vencer o atrito estático.
Depois, trocando o atrito estático pelo cinético e aplicando novamente a segunda lei, podemos achar a aceleração.
Mas relaxa, vou fazer passo a passo contigo!
Passo 2
Letra (a):
Aplicando a Segunda Lei de Newton aos eixos e , temos:
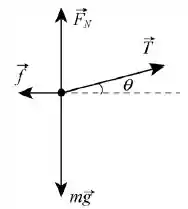
A primeira equação temos:
E a segunda nos dá:
Para que o caixote permaneça em repouso, devemos ter , ou seja, .
Se a tensão da corda é apenas suficiente para colocar o caixote em movimento, temos:
Assim:
O que nos dá:
Beleza até aqui galera? Bora continuar então!
Passo 3
Letra (b):
Aplicando a Segunda Lei de Newton aos eixos x e y, temos que:
Como , a segunda equação nos dá
Beleza?
Substituindo na primeira equação, obtemos:
E assim podemos obter a aceleração :
Substituindo pelos valores que já conhecemos:
E é isso! Espero ter ajudado!
