Você está segurando um livro contra uma parede vertical aplicando uma força com sua mão. O ângulo entre sua força e a vertical é , como mostra a figura abaixo. A massa do livro é e o coeficiente de atrito estático é . Se você empurrar forte demais, o livro começará a deslizar para cima e se você não aplicar força suficiente, o livro deslizará para baixo.
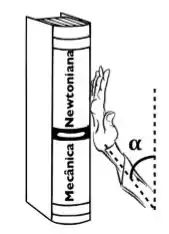
Esboce o diagrama de forças para os dois casos na situação em que o livro está prestes a deslizar.
Calcule a magnitude da força que você deve aplicar (como função de ) na iminência do movimento, também nos dois casos.
Calcule a magnitude da força aplicada (como função de ) para a qual a força de atrito se anula. Avalie o resultado para e .
Para um dado ângulo de aplicação da força, determine o intervalo de valores de em que ainda é possível fazer com que o livro deslize para cima.
Passo 1
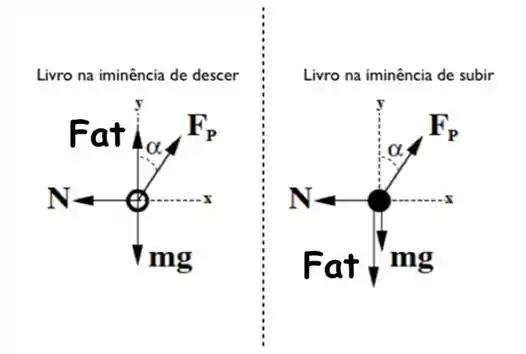
Onde corresponde a força de atrito, é a força de apoio que a mão está aplicando, é o peso do livro e é a reação normal.
Passo 2
Vamos começar pelo caso em que o livro está na iminência de deslizar para baixo, a força de atrito é dada por:
Decompondo a força nos eixos e , podemos analisar o movimento nas direções e . Como o livro está em repouso, o somatório das forças no eixo deve ser zero, assim como o somatório das forças no eixo . Portanto:
No eixo :
No eixo :
Substituindo o valor de que encontramos anteriormente:
Levando finalmente até:
O mesmo raciocínio pode ser aplicado para a situação de iminência de deslizamento para cima:
No eixo :
No eixo :
Substituindo o valor de que encontramos anteriormente:
Logo,
Passo 3
No item anterior, ao analisar o movimento no eixo na iminência de deslizar para baixo e para cima, encontramos as seguintes equações:
Em ambas as equações vemos que se a força de atrito se anula ficamos com a equação:
Quando (diretamente na vertical):
Quando (diretamente na horizontal):
Logo é impossível segurar o livro com uma força horizontal sem ajuda da força de atrito.
Passo 4
Como já vimos no item , a equação de equilíbrio na direção para que o livro deslize para cima é:
Portanto, o valor de pode variar de tal forma que não anule o denominador da fração. Porque ao anular o denominador, precisará de uma força infinita para equilibrar o livro. Portanto vamos descobrir em qual valor o anulará o denominador.
Logo, quando , você precisará aplicar uma força infinita ao livro. Logo,
Resposta
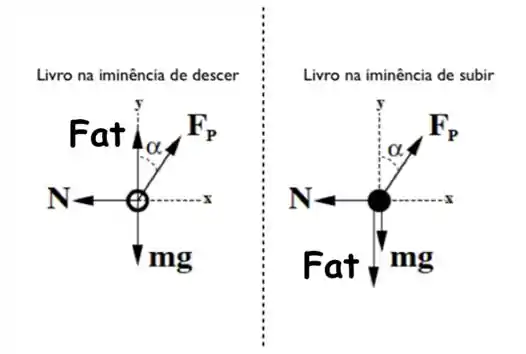
Na iminência de deslizar para baixo:
Na iminência de deslizamento para cima:
Quando (diretamente na vertical):
Quando (diretamente na horizontal):