Na figura, o fio e a roldana são ideais, e o plano fixo em que se apoia o bloco possui inclinação com a horizontal. Em todas as situações abaixo, o fio permanece tensionado e , mas o bloco pode variar. Quando necessário substituir valores, use .
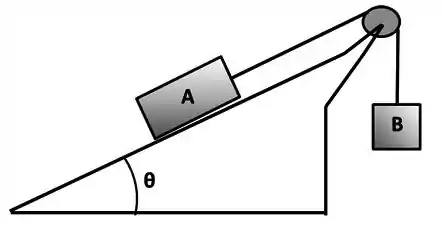
Neste item, . Pendurando-se vários blocos diferentes, descobriu-se que o peso máximo sem que o sistema entre em movimento é . Qual é o peso mínimo de que impede o deslizamento no sentido contrário?
Passo 1
Quando o peso de for mínimo estaremos na situação de iminência de movimento do bloco para baixo do plano, ou seja de para cima. Entretanto, o sistema ainda não se move, então a aceleração ainda é nula:
Nesse caso, a força de atrito estático entre o bloco e o plano será máxima , e terá a mesma direção e sentido da tração, pois elá estará se opondo a tendência de movimento. A equação de movimento do bloco será então (adotando um referencial positivo paraa cima da rampa):
Analogamente, quando temos o peso de máximo, estaremos na situação de iminência de movimento do bloco para cima do plano, desse modo a força de atrito estará no sentido oposto ao descrito acima, teremos portanto, a seguinte equação (adotando um referencial positivo para cima da rampa):
Para ambos os casos, a equação do bloco não sofre alteração. Teremos então:
Passo 2
Como nos foi dado o valor máximo de , iremos analisar esse movimento primeiro, para poder descobrir o valor da força de atrito estático máxima e então trabalhar na situação em que é mínimo.
Por estarmos no equilíbrio, temos que . Como ele nos diz que no caso do peso de máximo, , utilizando a equação do bloco , temos:
Substituindo o valor de e os outros valores conhecidos na equação de movimento do bloco quando temos máximo, temos:
Passo 3
Agora, que sabemos o valor da força de atrito estático máxima, podemos descobrir o valor mínimo de , basta substituirmos o valor da força na equação de movimento do bloco para mínimo.
Pela equação do bloco , temos:
Resposta