Uma caixa de massa está sob outra caixa, de massa . Uma pessoa tenta arrastar as caixas, puxando a de cima com uma força de módulo , que faz um ângulo com a horizontal, conforme a figura. Não há atrito entre a caixa debaixo e o solo e os coeficientes de atrito estático e cinético entre as duas caixas são, respectivamente, e . Observa-se que o sistema composto pelas duas caixas se desloca em conjunto para a direita com aceleração de módulo .
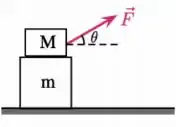
Podemos afirmar que o módulo da força de atrito entre os blocos é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
Vamos separar os blocos para analisar as forças em cada um deles.
Bloquinho de massa :
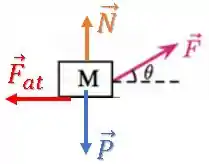
Decompondo a força , temos:
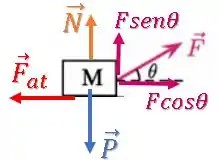
Como o bloco está em equilíbrio na vertical, o somatório de forças nessa direção é zero:
Opa, conseguimos a força normal ...
Como queremos encontrar a , a ansiedade ataca e a gente já acha que pode calcular a com:
ATENÇÃO! NÃO PODEMOS FAZER ISSO!

Bom, não podemos fazer isso pelo seguinte motivo:
Apenas quando a força de atrito estático atinge seu valor máximo que ela terá o valor de:
No caso do nosso problema, o bloquinho não necessariamente está quase deslizando, por isso, não necessariamente apresenta um valor de máximo.
Opa então como calculamos isso?
Passo 2
Voltando ao bloquinho de massa ...
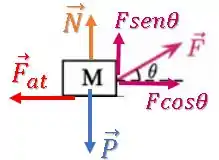
Podemos tentar também escrever segunda lei de Newton para as forças na horizontal:
Putz, mas se olharmos as alternativas, nenhuma delas têm esse valor... por mais que isso não esteja errado.
A questão só está nos forçando a achar de outra maneira.
Passo 3
Deixamos por último, porém essa era a maneira mais direta de achar a desde o início... não me bate hahaha.
Vamos olhar para as forças no bloco de massa agora.
Temos a força peso e normal .
Como a superfície entre o chão e o bloco não tem atrito, a única força de atrito será entre a superfície dos blocos, porém a força de atrito agora aponta no sentido contrário do outro bloco (ação e reação):
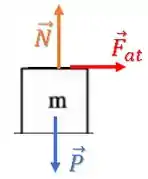
A força de atrito é a única força na horizontal, capaz de gerar a aceleração no bloco, então:
Simples assim, conseguimos a força de atrito .
Ficamos com a letra (a).
Resposta
Letra (a)