Uma caixa de massa é colocada em cima de uma caixa maior de massa como mostrado na figura. Quando uma força de módulo é aplicada na caixa grande, ambas as caixas se movem para a direita com a mesma aceleração. Supondo que o coeficiente de atrito entra as caixas é e que não há atrito entre a caixa maior e o chão, qual é a força atuando na massa menor?
a)
b)
c)
d)
e)
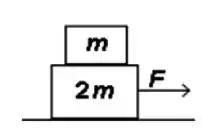
Passo 1
Sabemos que o bloco todo se move com uma aceleração constante , certo?
Ou seja, escrevendo a segunda lei do nosso amigo Nenê pro bloco todo, ficamos com:
Passo 2
Como a massa menor se move também com a aceleração , podemos escrever a equação da segunda lei do nosso amigo Nenê para ela assim:
Onde é a força de atrito.
Mas como sabemos que:
Podemos relacionar as duas forças dividindo uma equação pela outra:
Resposta
e)