UFRJ – Física 3 – 2020.2 – PF – M.Escolha
. Um capacitor de capacitância é conectado inicialmente a uma bateria e carregado até armazenar uma carga de . A seguir, o capacitor é desconectado da bateria e conectado a dois outros capacitores, inicialmente descarregados, de capacitâncias e , como mostrado na figura abaixo. Nessa situação, as cargas armazenadas nos capacitores e valem, respectivamente:
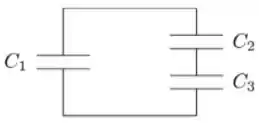
Escolha uma opção:
e
e
e
e
e
e
e
e
Passo 1
Vem comigo que a gente detona essa juntos!
Na situação que o enunciado nos descreve a gente tem um capacitor carregado então ele tem uma diferença de potencial dada por:
Então ele funciona como uma bateria para os capacitores e que estão em série. Por conta de os capacitores estarem em série a carga acumulada neles é mesma.
Então para char essa carga podemos usar a mesma equação de cima, mas agora a capacitância é a equivalente considerando e , ela vai ser dada por:
Vamos as contas!
Passo 2
Primeiro vamos calcular a diferença de potencial oferecida por , temos:
Então temos que:
Passo 3
Agora vamos calcular , temos:
Substituindo com os valores que conhecemos, temos:
Então:
Passo 4
E finalmente vamos calcular a carga nos capacitores, temos:
Então temos que:
Então nossa alternativa vai ser a letra .
Resposta
e