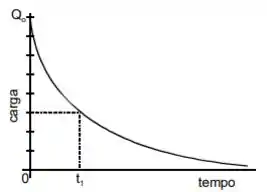
A figura abaixo representa o processo de descarga de um capacitor como função do tempo. No tempo , a diferença de potencial entre as placas do capacitor era . No instante de tempo , assinalado no gráfico, a diferença de potencial, em volts, entre as placas do capacitor é:
a) b) c) d) e)
Passo 1
No instante , a gente sabe que , e se a gente contar as linhazinhas do gráfico, a carga é . Então a gente pode usar a fórmula pra calcular a capacitância.
Aí no tempo , a carga é , e a capacitância a gente já sabe, ela continua a mesma porque é o mesmo capacitor. Então a gente consegue achar o :)
Passo 2
Em temos que
Então, em :
Boaa! Nossa alternativa correta é a letra C!!
Resposta
c)
Exercícios de Livros Relacionados
Os dois objetos de metal da Fig. 25-24 possuem cargas de + 70 pC e -70 pC, que resultam em uma diferença de potencial de 20 V. (a) Qual é a capacitância do sistema? (b) Se as cargas mudam para + 200 p
As placas de um capacitor de placas paralelas são separadas por uma distância d 0 e cada placa tem área A . Uma lâmina metálica d e área A é inserida entre as placas de maneira tal que a lâmina é para
Calcule:a) a capacitância de um par de placas paralelas com área de 100c m 2 cada, separadas de 3,0m m ;b) o campo elétrico quando o capacitor possui uma carga de 0,10μ C .
Um capacitor com placas paralelas no ar possui uma capacitância igual a 245 pF e um módulo de carga de 0,148 μ C em cada placa. A distância entre as placas é igual a 0,328 mm. (a) Qual é a diferença d
Na Figura 17.14, a chave comutadora está inicialmente na posição a . Calcule a carga Q 1 no capacitor de capacitância C 1 , após a chave ser comutada para a posição b e cessarem as correntes.