Indique com V se afirmação é verdadeira, ou F, se é falsa
a)_____ Aproxima-se uma partícula carregada de uma esfera condutora e neutra e isolada. Após restabelecido o equilíbrio eletrostático, a força eletrostática resultante sobre a esfera é nula, já que o campo eletrostático em qualquer ponto no interior da esfera é nulo.
b)_____ Um capacitor ideal, originalmente vazio, de placas quadradas, paralelas, tem suas arestas duplicadas, mantendo-se a distância entre as placas constante. Ainda que preenchamos tal capacitor com um material isolante qualquer, é impossível fazer a nova capacitância igual à antiga.
c)_____Em um condutor em equilíbrio eletrostático, o potencial elétrico tem o mesmo valor em todos os pontos de seu interior.
d)_____ Se o fluxo elétrico através de uma superfície fechada for zero, então não há partículas carregadas na região interior à superfície.
e)_____ De acordo com o princípio da superposição, o campo eletrostático criado por um sistema de partículas carregadas em um ponto de uma superfície fechada é dado pela soma vetorial apenas dos campos das cargas que estiverem dentro dessa superfície.
f)_____ O campo eletrostático em qualquer ponto de uma superfície equipotencial tem sempre o mesmo módulo, já que ele é sempre perpendicular a essa superfície.
g)_____ Se um capacitor é mantido isolado enquanto um material dielétrico é inserido em seu interior, sua energia armazenada diminui.
h)_____Um dipolo elétrico, formado por partículas de cargas e , separadas por uma distância fixa , encontra-se em uma região onde há campo eletrostático uniforme . Inicialmente, o seu momento de dipolo aponta na mesma direção e no mesmo sentido que o campo. O dipolo é girado de até ficar antiparalelo ao campo (mesma direção de , mas sentido oposto). O trabalho realizado pelas forças eletrostáticas sobre o dipolo, nesse processo, foi positivo.
i)_____ Duas linhas de campo elétrico nunca podem se cruzar.
j)_____ A lei de Gauss só é válida para distribuições de carga com algum tipo de simetria.
Passo 1
a) Para analisar este item, vamos considerar que uma carga se aproxima da esfera condutora, como mostra a figura abaixo. A presença dessa carga induz uma redistribuição das cargas positiva e negativa da esfera condutora neutra, cuja carga total é . Uma carga negativa se redistribui mais sobre a superfície direita da esfera, se aproximando de e outra carga se afasta de se distribuindo mais sobre a superfície à esquerda da esfera condutora, como mostra a figura.
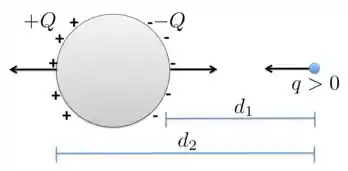
Como , da lei de Coulomb sabemos que a intensidade da força de aproximação entre e é maior do que a de afastamento entre e . Por isso, ainda que a esfera seja neutra, ou seja, , a presença de uma carga q resultará em um força resultante sobre a esfera diferente de zero.
b) Na primeira situação, a capacitância inicial é dada por
em que é a área inicial do quadrado de aresta e é a distância entre as placas do capacitor.
Na segunda situação, a aresta das placas dobra e temos e, por isso, a nova área é . Portanto, para a mesma distância entre as placas, a capacitância final é
Inserir um dielétrico nessa situação final faria com que a capacitância final fosse ainda maior do que , pois, como , teríamos
sendo impossível tornar a capacitância igual à inicial e isso torna este item VERDADEIRO.
Passo 2
c) No equilíbrio eletrostático, as cargas em excesso em um condutor se localizam sobre sua superfície, por isso, o campo elétrico no interior de seu volume é nulo.
O campo elétrico é proporcional à variação do potencial com a posição, ou seja, está relacionado à derivada do potencial em função das posições. Bom, como o campo elétrico dentro de um condutor em equilíbrio eletrostático é nulo, o potencial dentro desse condutor é constante e tem o mesmo valor em todos os pontos de seu interior.
Portanto, este item está CORRETO.
d) A lei de Gauss relaciona o fluxo do campo elétrico através de uma superfície fechada com a CARGA LÍQUIDA CONTIDA NO INTERIOR DESSA SUPERFÍCIE FECHADA. Isso significa que podem existir partículas carregadas dentro da superfície, mas se soma dessas cargas resultar em uma carga líquida nula, o fluxo será zero.
Portanto, o item está INCORRETO.
Passo 3
e) A lei de Gauss relaciona o fluxo do campo elétrico através de uma superfície fechada com a CARGA LÍQUIDA CONTIDA NO INTERIOR DESSA SUPERFÍCIE.
Cargas elétricas que estão fora da superfície fechada produzem campo elétrico em pontos sobre a superfície fechada. A grande questão aqui é que ESSAS CARGAS NÃO CONTRIBUEM PARA O FLUXO ELÉTRICO ATRAVÉS DA SUPERFÍCIE FECHADA.
É importante que você mantenha isso em mente: as cargas carregadas produzem campo elétrico e sempre vale o princípio da superposição para analisar o campo elétrico resultante produzido por essas cargas. AGORA, para o cálculo do fluxo elétrico através da superfície fechada, somente as cargas dentro dessa superfície contribuem.
f) Como discutimos no item c) acima, o campo elétrico dentro de um condutor EM EQUILÍBRIO ELETROSTÁTICO é nulo e, por isso, o potencial dentro dele é constante.
Além disso, o campo elétrico de um condutor qualquer em equilíbrio eletrostático é sempre perpendicular à sua superfície em todos os seus pontos. NO ENTANTO, PORÉM, TODAVIA, a intensidade desse campo elétrico NÃO NECESSARIAMENTE é o mesmo em todos os pontos da superfície.
Para você não se esquecer desse NÃO NECESSARIAMENTE, lembre-se, por exemplo, do “poder das pontas” de condutores em equilíbrio eletrostático: superfícies com áreas menores acumulam mais cargas estáticas e, portanto, produzem campos elétricos mais intensos. Então, podemos ter condutores cujas áreas superficiais não são uniformes e, por isso, eles têm campos elétricos perpendiculares à suas superfícies com intensidades diferentes ao longo de sua extensão. Por essa razão, este item está INCORRETO!
Passo 4
g) Quando um dielétrico é inserido em um capacitor, a capacitância inicial deste capacitor aumenta por um fator constante e seu novo valor é . Isso é equivalente a dizer que a nova permissividade do meio material entre as placas aumenta para.
Por outro lado, se esse capacitor é mantido isolado, ou seja, se as cargas sobre suas placas são sempre as mesmas, então, como
onde é a ddp entre as placas, o potencial inicial tem que diminuir para . Se o potencial diminui dessa maneira, então o campo elétrico inicial também diminui para , ou seja, diminui pelo fator que o potencial.
Agora, como a densidade de energia inicial armazenada no campo elétrico do capacitor sem o dielétrico é dada por
a nova densidade energia armazenada no campo após a introdução do dielétrico é
Portanto, como a constante dielétrica é , ao inserirmos o dielétrico no interior do capacitor, a quantidade de energia armazenada em seu volume diminui.
O item g) está CORRETO.
h) Como o campo elétrico é uniforme, então a energia de interação entre um dipolo elétrico e esse campo é dada
Na primeira situação descrita, temos paralelo à (portanto, a ângulo entre eles é zero!) e, lembrando que o produto escalar entre dois vetores quaisquer e é dado por: , com sendo o ângulo entre eles, a energia pode ser escrita como
Na segunda situação, é antiparalelo à , ou seja, o ângulo entre eles é de . Por isso, a energia é
Como o campo eletrostático é um campo conservativo, o trabalho realizado pelo campo para levar o dipolo a ficar antiparalelo ao campo, é dado por
que é negativo, o que torna este item INCORRETO!
Passo 5
i) Se duas linhas de campo se cruzassem, isso significaria que neste ponto de interseção poderiam ser definidos dois campos diferentes o que não pode ocorrer. Por isso, este item está CORRETO!!
j) A lei de Gauss é válida sempre, independente se o problema em análise tem alguma simetria ou não. Em problemas com simetria, ela facilita, em muito, a obtenção do campo elétrico das respectivas distribuições de cargas. Portanto, este item está INCORRETO.
Resposta
- F
- V
- V
- F
- F
- F
- V
- F
- V
- F