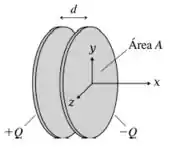
Um capacitor é um dispositivo eletrônico formado por duas placas metálicas idênticas, carregadas com cargas , separadas por um distância conforme ilustrado na figura abaixo.
Capacitores comerciais são construídos com placas cujos diâmetros são muito maiores que a separação e são de grande interesse em aplicações de eletrônica. Considerando esses capacitores comerciais, assinale a opção que melhor descreve o potencial eletrostático entre as placas carregadas .
Passo 1
Primeiro, é importante nos lembrarmos de algumas características de um capacitor de placas paralelas. Como o diâmetro das placas é muito maior do que a distância entre elas, então, o campo elétrico na região entre as placas é uniforme, ou seja, tem o mesmo valor em todos os pontos.
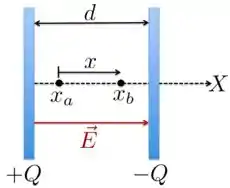
Outra característica é que vetor campo elétrico tem sempre direção perpendicular às placas e seu sentido é sempre da carga positiva para a carga negativa . Isso está desenhado na figura abaixo, que mostra o capacitor visto de perfil.
Passo 2
Uma vez que resumimos as características de dentro do capacitor, vamos olhar, agora, para os pontos e da figura, que estão a uma distância um do outro, e calcular a diferença de potencial elétrico entre as placas.
A diferença de potencial elétrico é dada por
Vamos considerar o elemento de comprimento paralelo ao campo elétrico . Juntando essa informação com o fato de ser uniforme na região entre as placas e colocando tudo dentro da expressão acima, teremos o seguinte:
Se fazemos , a diferença de potencial fica:
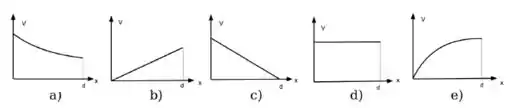
que é uma função linear crescente da distância dentro da região entre as placas.
Por isso, o gráfico que representa o potencial tem que ser uma reta crescente de .
Resposta
Letra b.